Využití alternativních výpočetních prostředků ke zkvalitnění studijní průpravy studentů

Tomáš Barot
Fakulta aplikované informatiky
Ústav řízení procesů
e-mail: barot@fai.utb.cz

Abstrakt

Článek popisuje přínosy vyššího doporučování alternativních výpočetních programů vysokoškolským studentům. Zdůrazňuji ale, že tento metodický postup kategorizuji jako doplněk k již existujícím metodám VŠ. Nesnažím se upřednostňovat postup před ostatními postupy. Předkládaný návrh by měl být uplatněn pouze v součinnosti s již zavedenými metodami. Článek hodnotí v teoretické rovině přínosy i negativa využívání konkrétních alternativ programů Matlab [1] a Mathematica [2]. Tyto alternativní programy byly popsány v celé řadě publikací. Proto není mou snahou je zde uvádět jako novinku, ale poukázat na jejich vyšší využitelnost při přípravě na výuku na straně studentů. Hodnotím aspekty přínosu konkrétních programů u vybraných odborných předmětů na FAI UTB ve Zlíně. Avšak při zvyšující se odbornosti předmětu doporučuji využívat alternativních nástrojů v menší míře. Neposkytují obvykle natolik specifické funkce, které standardně nabízí komerční nástroje. Především ale zdůrazňuji, že je velmi důležité apelovat na studenty již v rané fázi jejich vysokoškolského studia. Může se tím zamezit případům, kdy student plynule neporozumí novým matematickým teoriím, na které pak navazují konkrétní aplikace v dalších odborných předmětech. Tyto skutečnosti se snažím objektivně hodnotit v předkládaném článku se závěrem, že praktické nasazení postupu může přinést veskrze pozitivní výsledky v oblasti vzdělání studentů.

Abstract

The article describes the advantages of the more intense utilization of alternative computing programs by the university students. But I emphasize, that I categorize this method as the complement of already existing university methods. I don't try to prefer the described method to the other methods. The proposed method should be only applied with the already established methods. The article theoretically evaluates the advantages and disadvantages of the concrete alternatives of Matlab [1] and Mathematica [2]. This alternative programs were described in many publications. That's why my tendency isn't present them as the innovative solution, but I want to point out their more intense utilization for the student learning support. I evaluate the positive aspects of the concrete programs on the specialized subjects at the FAI TBU in Zlin. I recommend to utilize the alternative programs on the reduced scale in the cases with the graduating subject specialization. They usually don't offer more specific functions as the commercial programs. I primarily emphasize, that is very important to appeal to the students in the beginning phase of their university studies. It is also the prevention for the problems with the absence of the new mathematic theories understanding and their application ability in the consequential specialized subjects. I try to objectively discuss this facts in this presented article with the conclusion, that the practical utilization of this method can bring thoroughly the positive aspects in the area of the student education.

Podstata návrhu zkvalitnění studijní průpravy studentů a jeho začlenění do souboru již zavedených metod VŠ ve formě doplňku

Návrh metody si klade za cíl zlepšit matematicko-teoretické povědomí studentů sdůrazem na podporu přípravy na výuku. Hlavní myšlenkou je působení na studenty, aby využívali také výhod alternativních matematicko-výpočetních programů při vstřebávání nových teoretických poznatků. Je třeba, aby o této možnosti věděli a byli cíleně informováni. Přitom nezpochybňuji kvalitu úrovně komerčních produktů. Jen nahlížím na alternativní matematický SW jako na vhodný doplněk při přípravě na výuku. V rámci vzdělávacího procesu by mělo být více apelováno na studenty, aby pro zdokonalení svých matematických dovedností tento postup uplatňovali. Podotýkám, že tak lze činit již vrané fázi studia na VŠ. Pokud se student obecně naučí prakticky pracovat smatematickým SW, bude mít matematickou teorii lépe zažitou. Nebude mu činit problémy aplikovat poté své poznatky vodborných předmětech, u nichž se znalost matematického aparátu předpokládá. Na FAI UTB ve Zlíně například vodborných předmětech Teorie systémů, Optimalizace, Modelování a identifikace náhodných procesů. Pokud precizněji student pochopí náplň kapitol algebry, diferenciálního a integrálního počtu reálné funkce více reálných proměnných a okruhu řešení obyčejných diferenciálních rovnic, pak snáze prakticky aplikuje své znalosti v konkrétních případech. Po zvládnutí činnosti valternativních programech nebude mít student problémy pochopit práci skomerčními matematicko-výpočetními programy. Zafixování významu použití volně dostupných matematických nástrojů do povědomí nastupujících studentů by mělo teoreticky přinést vyšší úspěšnost při absolvování odborných předmětů obecně, neboť matematika je pro vysokoškolské studium nezbytným základem. Nepřináším informace o volně dostupných alternativních nástrojích jako novinku, ale poukazuji na možnost jejich aplikace, což vpozitivním důsledku může podpořit kvalitu celkového vzdělávání technického směru. Dále také pojednávám o posouzení možností konkrétního nasazení vybraného alternativního SW pro domácí teoretickou přípravu studentů FAI UTB ve Zlíně. Na následném obrázku (Obr.1.) uvádím schéma začlenění navrhovaného postupu do komplexu již zavedených metod VŠ spolu sgrafickým vyjádřením metody jako doplňku. Dále znázorňuji skutečnost, že pro celkové zlepšení kvality vzdělání studentů je nutnou podmínkou, aby jednotlivé části diagramu byly ve vzájemné interakci a souhře, neboť větší úspěch přinese doplňující se komplex metod. Samotná metoda, kterou zde navrhuji by osamocena zcela ztratila na významu. Existující kvalitní a odborná výuka VŠ je nesporně základním stavebním kamenem vzdělávacího systému. Velmi kvalitní výuka matematiky je na FAI UTB ve Zlíně, kdy je kladen důraz na zlepšení úrovně technických vědomostí studentů již před nástupem na VŠ ve formě přípravných kurzů na přijímací zkoušky.

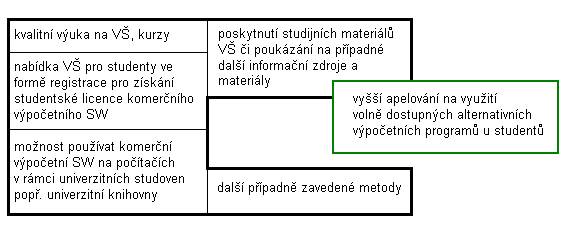
Obr.1. Začlenění využití alternativního SW, jakožto doplňku k již zavedeným metodám

Přehled vybraných volně dostupných alternativních výpočetních programů

Program FreeMat [3] je volně dostupné prostředí pod GPL licencí. Slouží pro vědecké výpočty a zpracování dat. Snaží se přiblížit komerčnímu programu Matlab. Na stránkách projektu se udává 95% kompatibilita funkcí Matlabu sprogramem FreeMat. Program zahrnuje i řadu funkcí nad rámec Matlabu. Příkladem může být možné rozšíření zdrojových kódů o příkazy jazyků C, C++, FORTRAN. O programu FreeMat byla napsána na FAI UTB ve Zlíně bakalářská práce, kterou vytvořil Pavol Turan [6]. Instalace programu je možná zinternetových stránek projektu FreeMat, a to ze zdroje [4]. Vsekci Download se nachází možnost stažení instalačního programu pro různé operační systémy. Ve zmíněnékategorii je také dostupná dokumentace programu vanglickém jazyce veformě PDF souboru. Je ji možné najít též na hlavní stránce projektu v sekci Documentation v podobě HTML stránek. [4][5]

Program GNU Octave [7] je také jako program FreeMat multiplatformní. Domovská stránka projektu se nachází na zdroji [8]. Ke stažení instalačního souboru pro konkrétní operační systém se uživatel dostane skrze odkazy na hlavní stránce projektu [8]. Výběr součástí, které jsou pro program nadstavbové, a to v tzv. formě packages, lze provést přímo v dialozích instalačního průvodce. Přidání programu například na distribuci Linux Ubuntu lze provést jednoduše přes menu Aplikace > Přidat/Odstranit aplikace.Všechny podstatné údaje o možnostech rozšíření pogramu uživatel najde na stránkách projektu [8], o grafickém rozšíření například na zdroji [9]. Pokud jde o účel programu jako takového, tak je určen pro numerické výpočty. Ovládání programu je umožněno prostřednictvím příkazového řádku. Tvůrci na svých stránkách uvádí, že příkazy jsou majoritně kompatibilní s programem Matlab. Program GNU Octave je volně dostupný, a to pod licencí GPL. Umí řešit velké množství matematických problémů. Postup práce s programem je názorně popsán na stránkách zdroje [10]. Na zdroji [11] se nachází příklady specifického využití rozšiřujících možností programu, a to k řešení úloh z oblasti teorie automatického řízení. Zdroje [10] a [11] jsou praktické výsledky kvalifikačních prací studentů FAI UTB ve Zlíně zaměřené na práci s programem. [8]

Program Scilab [12] má v oblasti alternativních výpočetních nástrojů největší věhlas. Volně dostupný je pro školní či domácí využití. Tvůrci programu doporučují používat nástroj pro výuku matematiky a pro výuku obecně jako takovou. Důkazem kvality programu Scilab je jeho nasazení na řadě vysokých škol. Konkrétně v Číně, Indii a Japonsku, Francii. Nejvíce dostupných informací o programu najde uživatel na samotných stránkách programu Scilab, a to na zdroji [13]. Nápověda k funkcím programu se nachází ve formě HTML stránek na zdroji [14]. Projekt Scilab je nástrojem multiplatformním. Stažení programu pro konkrétní operační systém je možné skrze hlavní stránku projektu, a to prostřednictvím menu Products > Download. Celkové využití programu je možné v širokém spektru vědních oborů. Kromě typických technicky orientovaných odvětví je možné jej uplatnit například také v lékařství i biologii. Program lze s výhodou používat také v zaměřeních týkajících se řízení, simulace, optimalizace, zpracování signálu a v celé řadě dalších. Výhodou programu je integrované návrhové a simulační prostředí Xcos, což je jeho velkým pozitivem. Pro program existuje řada rozšiřujících možností pro jeho konkrétnější praktická uplatnění. [13] [15]

Program Maxima [16] je též volně dostupné výpočetní prostředí, které je svým ovládáním blízké programu Mathematica. Projekt Maxima je prezentován a nabízen ke stažení na zdroji [17], což je jeho hlavní internetový portál. Opět se zde jedná i v tomto případě o multiplatformní nástroj. Na distribuci Linux Ubuntu jej lze přidat stejně jako program GNU Octave skrze menu systému Aplikace > Přidat/Odstranit aplikace. Program Maxima je systémem, který pracuje především se symbolickými výrazy. Samozřejmostí je podpora numerických funkcí a operací, které spadají do oblasti algebry i matematické analýzy. Program se vyznačuje vysokou přesností číselných výsledků. Spíše než-li na Matlab se vývojově orientuje na směr, který udává program Mathematica. Bohatá dokumentace k nástroji Maxima je dostupná v sekci Documentation zdroje [18]. [17]

 

Program JMathLib [19] má internetovou prezentaci se sekcemi Download a Documentation na zdroji [20]. Na stránkách je uvedeno, že je cílem projektu jít ve stopách programů Matlab, FreeMat, Scilab a GNU Octave. Program autoři označují za klon programu Matlab. Výpočetní nástroj je naprogramován v jazyce Java. Množinu dostupných matematických funkcí doplňují specializované balíky - toolboxy. Prostředí se může používat psaním příkazů přímo do okna terminálu nebo interpretací skriptovacích souborů, což jsou klasické způsoby práce s výpočetními nástroji toho typu. Pro běh programu je potřeba mít nainstalováno rozhraní Java Runtime Environment. [20]

Uvedené nástroje jsou v určitých aspektech navzájem odlišné, v některých dokonce velmi příbuzné. Rozdíly můžeme obecně najít v tom, jaké matematické funkce dané nástroje podporují a nabízí. I když svým vývojem k dokonalosti komerčních programů pouze směřují, tak i přesto je řada z nich na velmi vysoké úrovni. Obecně mají všechny uvedené alternativní nástroje velké pozitivum v tom, že jsou snadno a volně dostupné studentům. Na tuto skutečnost bych kladl důraz. Ale s nutným upozorněním, že ne všechny nástroje se dají za všech okolností použít. V tomto případě je již nutné používat komerčních nástrojů. K absenci specifických funkcí u volně dostupných nástrojů dochází. Proto dále uvádím konkrétní zhodnocení možného nasazení alternativních nástrojů u vybraných odborných předmětů na FAI UTB ve Zlíně. Celkově je třeba pohlížet na uváděná fakta ve smyslu doplňkových možností průpravy studentů na výuku, jak jsem uvedl na schématu (Obr.1).

Hodnocení přínosu možného využití vybraných programů v odborných předmětech na FAI UTB ve Zlíně

Předmět Matematika I se ve své podstatě zabývá reálnými funkcemi jedné reálné proměnné. Vyšetřují se zde průběhy funkcí, počítají jejich limity, derivace. Studenti řeší výpočet neurčitých a určitých integrálů. Probírána je vpředmětu též výroková logika, teorie množin, diferenciál funkce, nevlastní integrál a další důležité náležitosti teorie, která se týká oblasti funkcí jedné reálné proměnné. Nasazení alternativních programů při studijní průpravě na tento předmět je podle mne u nově nastupujících studentů významným krokem ke zkvalitnění jejich matematického povědomí. Studenti si kromě zobrazení samotných grafů funkcí mohou nechat vypočítat hodnoty limit, tvary derivací (obecně n-tého řádu), tvary neurčitých integrálů a také hodnoty určitých integrálů. Vyzkoušení výpočtů vtěchto programech může být i přínosem při klasickém počítání cvičebních příkladů. Nejen že studenti mohou své výsledky snadno ověřit, ale také mohou provést jejich grafickou vizualizaci. Znázornění vypočítaných výsledků také podpoří jejich grafickou představivost, která je po vysokoškolských studentech vyžadována. Průběh funkce bylo možné vykreslit všemi nástroji. U programu GNU Octave pro vykreslení grafu bylo nutné se zpříkazového terminálu přesunout do programové součásti WGnuplot. Pro symbolické výpočty derivací a neurčitých integrálů bych vyzdvihl používání nástroje Maxima, neboť je pro symbolické výpočty určen. Vjiných nástrojích jsem funkci pro symbolické výpočty hledal obtížně. Úlohy nesymbolického charakteru snadno řešily i ostatní nástroje (například stanovení hodnoty určitého integrálu). Všechny požadavky na řešení úloh předmětu Matematika I splňuje především program Maxima, který bych pro přípravu na tento předmět doporučil.

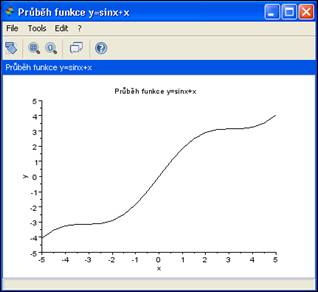
Obr.2. Průběh reálné funkce jedné reálné proměnné vprostředí Scilab

Obr.3. Výsledky matematických operací vprogramu Maxima

Předmět Matematika II navazuje na předmět Matematika I, a to s tím že se již nepracuje sreálnými funkcemi jedné reálné proměnné, ale sreálnými funkcemi obecně více reálných proměnných. Studenti projdou teoriemi stanovení definičních oborů, limit, parciálních derivací, totálního diferenciálu, výpočtem dvojných a trojných integrálů a samozřejmě vyšetřováním průběhů funkcí více reálných proměnných. Pro vyšetřování průběhu těchto funkcí bych právě jako doplněk doporučil použít volně dostupných nástrojů. Studenti mohou pro vyšetřování průběhů funkcí využít i příkazů patřících do samostatné oblasti spadající pod předmět Optimalizace. Tím si student může ověřit ručně vypočítané extrémy funkcí. Program Maxima zahrnuje funkci pro vyčíslení hodnoty dvojného integrálu. Výpočet trojného integrálu jsem zde ale již nenašel. Též jsem nenašel příkaz na řešení limity funkce více proměnných. Alternativních nástrojů bych vtomto předmětu využil pro vykreslování funkčních průběhů, kdežto na numerické a symbolické výpočty bych upřednostnil komerční nástroje. Ale spíše než-li Matlab, tak raději program Mathematica. Matlab nemá zahrnut grafický návrhář symbolických matematických výrazů, jak je tomu vprogramu Mathematica. Dále kromě vykreslení průběhů funkcí by se alternativní nástroje daly využít pro kontrolu stanovení extrémů funkcí metodami zpředmětu Optimalizace. Řada alternativních nástrojů zahrnuje své rozšíření právě pro oblast optimalizace.

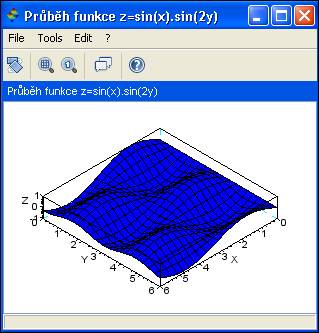
 Obr.4. Průběh reálné funkce dvou reálných proměnných vprostředí Scilab

Vpředmětu Diferenciální rovnice (dříve Matematika III) řeší studenti problematiku stanovení obecných a partikulárních řešení obyčejných diferenciálních rovnic, případně jejich soustav. Následuje také problematika číselných a funkčních řad. Obyčejné diferenciální rovnice jsou řešeny analyticky. Způsob analytického řešení je protikladem knáplni předmětů Teorie systémů a Simulace systémů. Chci tím říci, že vTeorii systémů se pro řešení ODR využívá svýhodou Laplaceovy transformace a vSimulaci systémů se probírá nikoliv analytické řešení ODR, nýbrž numerické. Pokud řeší student ODR analyticky, jistě uvítá možnost ověřit si své výsledky pomocí příkazů nacházejících se valternativních programech. Program Maxima, neboť zahrnuje podporu symbolických výpočtů, vrací výsledky řešení ODR vžádaném symbolickém tvaru. Ostatní alternativní nástroje, např. FreeMat, umí řešit ODR numericky s výsledkem ve tvaru číselné posloupnosti hodnot. Tyto hodnoty lze poté vykreslit do grafu, ale symbolický tvar výsledku zněj zpětně neurčíme. Proto bych vtomto předmětu doporučil využít zejména program Maxima.

Obr.5. Symbolický výsledek řešení ODR 1. řádu a ODR 2. řádu vprogramu Maxima

Předmět Základy matematiky zahrnuje průpravu studenta pro oblast lineární algebry, maticového počtu a řešení soustavy lineárních rovnic. Vpřípravě na tento předmět mohou bez váhání studenti využít kompletní škálu výše uvedených alternativních nástrojů. Skutečnost, která byla důležitá u výpočtů voblasti diferenciálního a integrálního počtu, a to nutnost vypočítat programem výsledky do symbolické formy, zde není prvořadou záležitostí. Výpočty se především týkají numerické oblasti. Práci smaticemi umožňují všechny výše uvedené volně dostupné nástroje. Neupřednostňoval bych zde žádný alternativní nástroj před nástroji ostatními, záleží vtomto ohledu pouze na výběru nástroje samotným studentem.

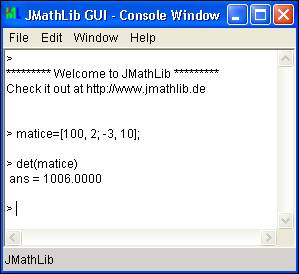
Obr.6. Výpočet determinantu matice vprogramu JMathLib

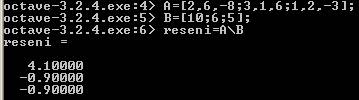
Obr.7. Řešení soustavy algebraických lineárních rovnic vprogramu GNU Octave

Optimalizace je předmětem bakalářského stupně studia, který vyžaduje po studentech, aby byli schopni určit extrémy funkcí a řešit další specifické úlohy s optimalizací spojených. Kromě analytických a iteračních optimalizačních metod je probíráno také lineární, celočíselné, dynamické programování. Řada volně dostupných alternativních programů nabízí základnu příkazů i pro řešení optimalizačních úloh. Mnoho iteračních metod si lze naprogramovat sice ručně, ale nyní budu klást důraz především na metody, které výpočetní nástroje nabízí ve formě jednorázově volatelných příkazů. Takové možnosti pak mohou využít také studenti předmětu Matematika II, a to ke kontrole analyticky určených extrémů reálné funkce více reálných proměnných. Doporučil bych pro hledání extrémů funkcí použít nástroj Scilab a pro specifické úlohy optimalizace program GNU Octave.

Obr. 8. Hledání globálního minima účelové funkce vprogramu Scilab

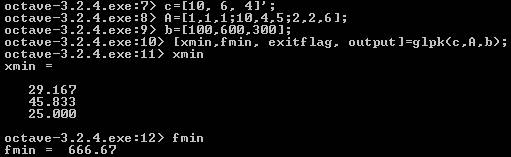
Obr.9. Řešení úlohy lineárního programování vprogramu GNU Octave

Předměty Automatizace a Teorie systémů si kladou za cíl, aby studenti získali přehled o spojitém i diskrétním automatickém řízením jako takovém. Dále je požadována po studentech schopnost systémy analyzovat, navrhovat a také simulovat.  Předmět se opírá o matematický aparát, který již má mít student zažitý a dále jej rozšiřuje o okruhy témat, které je nutné znát pro porozumění problematiky automatického řízení v komplexním ohledu. Analýzu a syntézu provádí studenti výpočetně v programu Matlab, v jehož součásti Simulink tvoří obvodová zapojení. Z důvodu, že teoretické náležitosti studenti simulují v prostředí Simulink, doporučím ze škály volně dostupných nástrojů pouze Scilab se součástí Xcos. Xcos je nástroj podobný programu Simulink. Zahrnuje programovou podporu pro účely návrhu jak spojitých obvodů řízení, tak i diskrétních. Na obrázku (Obr.10) uvádím příklad vytvoření návrhu regulačního obvodu, kterým je realizace zapojení zpětnovazebního regulačního obvodu s tzv. Smithovým prediktorem. Smithův prediktor plní významnou funkci kompenzace dopravního zpoždění. V programu Scilab – součásti Xcos lze navrhovat i diskrétní regulační obvody. Samozřejmostí je tvorba elektronických obvodů. Samotný Scilab má také výpočetní možnosti. Program zahrnuje řadu příkazů pracujících se spojitými i diskrétními popisy systémů. Dostupné funkce pro práci smaticemi jsou užitečné u řešení mnohorozměrových systémů. Algebraická podpora umožňuje realizovat algebraickou teorii řízení. Z obrázku (Obr. 11) je patrné, že se v programu Scilab nachází speciální příkazy využitelné právě v teorii řízení. I jiné volně dostupné programy mohou být teorii systémů programovou oporou. Příkladem může být podpora automatického řízení v rámci programu GNU Octave, jak uvádí zdroj [11]. I když je program Scilab vynikajícím nástrojem, má program Matlab v tomto odborném odvětví své dominantní postavení.

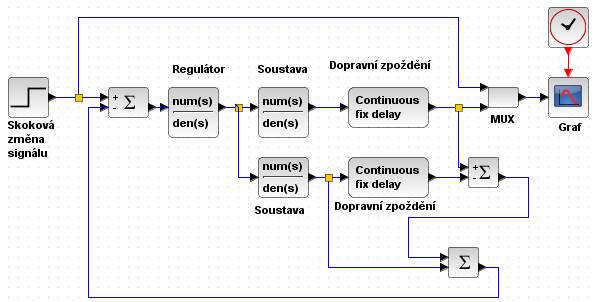
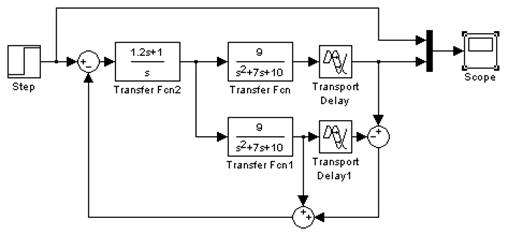
Obr.10. Realizace zpětnovazebního regulačního obvodu s použitím Smithova prediktoru pro kompenzaci dopravního zpoždění vprogramu Scilab/Xcos a vMatlab/Simulinku

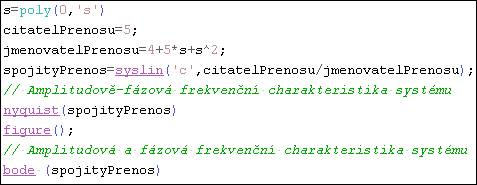
Obr.11. Vprogramu Scilab lze vykreslit charakteristiky vnějšího popisu spojitého systému

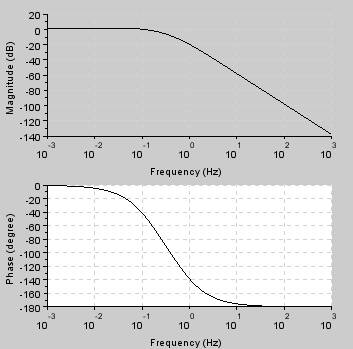
Obr. 12. Vykreslení amplitudové a frekvenční charakteristiky vprogramu Scilab

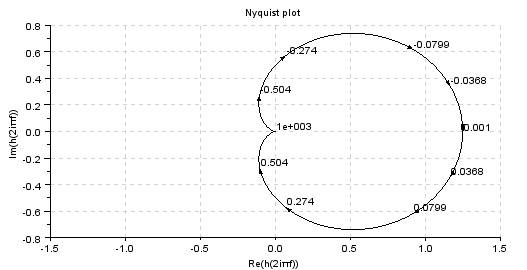
Obr.13. Vykreslení amplitudově-fázové charakteristiky vprogramu Scilab

V odborném předmětu Modelování a identifikace náhodných procesů studenti popisují matematicko-statistickým aparátem náhodné procesy, které aplikují při identifikaci systému. Příkladem identifikační metody, se kterou se studenti seznamují je metoda nejmenších čtverců. Metoda nejmenších čtverců má dvě varianty - rekurzivní a přímou. Obě metody umožňují na základě naměřených dat určit odhady parametrů modelu systému. Pro identifikační metodu nejmenších čtverců u modelu systému ARX, pro který je určen příkaz Matlabu arx(), jsem v programu Scilab alternativní příkaz nenašel. Je zde pouze identifikace pro model systému ARMAX. Také se mi nepodařilo najít ekvivalent příkazu Matlabu cra() pro identifikaci systému korelační metodou, která vrací jako výsledek vnější popis systému v podobě impulsní funkce. Tím se potvrzuje logická skutečnost, že při růstu odbornosti předmětu ubývá podpora ze strany alternativních programů. Volně dostupné programy bych použil například pro ruční naprogramování identifikačních metod za pomocí příkazů pro práci s maticemi. Pro rychlé provedení metod z oblasti identifikace systému bych raději doporučil Matlab, neboť zahrnuje širší podporu i pro odbornější technické aplikace, kterou je i tento předmět.

Závěr

V předkládaném článku navrhuji metodu zkvalitnění matematických znalostí studentů, a to formou vyššího apelování, aby při své přípravě na výuku, především však při studiu matematiky, více využívali volně dostupných alternativních matematicko-výpočetních nástrojů. Pokud by se navržený postup aplikoval spolu sjiž existujícími metodami, přínosem by bylo zlepšení znalostní základny vysokoškolských studentů. Předkládaný postup by mohl existovat pouze jako doplněk zavedených metod VŠ, kterými je kvalitní specializovaná výuka, kurzy, umožnění práce skomerčními výpočetními programy na studovnách VŠ, nabídka registrací studentských licencí komerčních programů. Cílem je tedy zlepšit kvalitu studijní průpravy vysokoškolských studentů. Zejména bych viděl kladný přínos při využití volně dostupných nástrojů u nově nastupujících studentů. Pokud nově nastupující studenti své metody přípravy na výuku rozšíří o nové způsoby, vytvoří si kvalitnější matematicko-teoretický základ, který budou moci lépe aplikovat vodborných předmětech. Zde je znalost matematického aparátu a schopnost jeho aplikování nezbytná. Rešerší vybraných volně dostupných nástrojů poukazuji na jejich existenci, ale neuvádím je jako novinku, neboť o nich bylo publikováno mnoho článků. Přehledem poukazuji na snadnou dostupnost nástrojů studentům. Velkým kladem je také multiplatformní charakter programů. Pokud si student osvojí práci sdokumentací, nebude mu činit potíže ke svému prospěchu sprogramy pracovat. Praktickou částí článku je ukázka možné aplikace alternativních programů ve vybraných odborných předmětech na FAI UTB ve Zlíně. Vpraktickém hodnocení uvádím programy, které se mi zdály nejlépe pro daný předmět uplatnitelné. Zjistil jsem také, že vněkterých případech programy požadované funkce nenabízí. Pak bych na řešení problémů nasazoval pouze komerční programy, jejichž podpora specifických oblastí je význačná. Ve většině případů byly ale alternativní programy schopny provádět i velmi specifické operace. Příkladem může být součást Xcos programu Scilab, která umožňuje navrhovat a simulovat regulační obvody, jak spojité, tak i diskrétní. Pro symbolické výpočty byl vhodný program Maxima, neboť ostatní alternativní programy vykazovaly pouze numerická řešení. Při řešení použitelnosti nástrojů u příkladu mnohem odbornějšího předmětu Modelování a identifikace náhodných procesů se již potvrdila skutečnost, že při vzrůstající specifičnosti oblastí problémů je vhodné používat veskrze komerčních programů. Při studiu možného praktického využití navrhované metody na FAI UTB ve Zlíně jsem ověřil vesměs kladné vlastnosti alternativních nástrojů. Vyšší apelování na využití alternativních nástrojů, ve smyslu doplňku kjiž zavedeným postupům, může být tedy pro vysokoškolské studenty technického směru přínosné, a to je hlavním cílem předkládaného návrhu metody ke zkvalitnění studijní průpravy studentů.

Použité zdroje

[1] The Mathworks. MATLAB,  Simulink [počítačový program].
[2] Wolfram Research. Mathematica [počítačový program].
[3] FreeMat [počítačový program]. Ver. 4.0.       Dostupný z <http://freemat.sourceforge.net/download.html >.
[4] FreeMat - Home [online]. poslední revize 24.10.2009 [cit. 2011-03-18].      <http://freemat.sourceforge.net>.
[5] FreeMat - FAQ [online]. poslední revize 24.10.2009 [cit. 2011-03-18].      <http://freemat.sourceforge.net/faq.html >.
[6] TURAN, P. Elektronický manuál pro program FreeMat. Zlín: Univerzita Tomáše Bati ve       Zlíně. Fakulta aplikované informatiky. Ústav aplikované informatiky, 2008. 70 s. Vedoucí       bakalářské práce Ing. Petr Navrátil, Ph.D.
[7] GNU Octave [počítačový program]. Ver. 3.2.4.  Dostupný z <http://www.gnu.org/software/octave/>.
[8] Octave [online]. poslední revize 8.2.2011 [cit. 2011-03-18].     <http://www.gnu.org/software/octave/>.
[9] PROKOP, David. Octave graphic add-on [online]. poslední revize 4.2.2008  [cit. 2011-03-18]. <http://www.grafickenadstavbyoctave.wz.cz>.
[10] JUST, Michal. Octave – český průvodce programem [online].  poslední revize červen 2006 [cit. 2011-03-18]. <http://www.octave.cz>.
[11] HALBSGUT, Martin. OCTAVE CONTROL SYSTEMS TOOLBOX [online]. poslední         revize 15.5.2007 [cit. 2011-03-18]. <http://ocst.yc.cz>.
[12] Scilab [počítačový program]. Ver. 5.3.1.  Dostupný z <http://www.scilab.org>.
[13] Scilab [online]. [cit. 2011-03-18]. <http://www.scilab.org>.
[14] Scilab Online Help [online]. poslední revize 3.3.2011 [cit. 2011-03-18].  <http://help.scilab.org>.
[15] ČERNÝ, Michal. Scilab: simulace i výpočty s toolboxy [online].   poslední revize 25.5.2011 [cit. 2011-03-18].   <http://www.root.cz/clanky/scilab-simulace-i-vypocty-s-toolboxy/>.
[16] Maxima [počítačový program]. Ver. 5.18.1.  Dostupný z <http://maxima.sourceforge.net/download.html>.
[17] Maxima, a Computer Algebra System [online].  poslední revize 7.8.2010     [cit. 2011-03-18]. <http://maxima.sourceforge.net>.
[18] Documentation // Maxima CAS [online].  poslední revize 9.3.2011   [cit. 2011-03-18]. <http://maxima.sourceforge.net/documentation.html>.
[19]  JmathLib [počítačový program]. Ver. 0.9.4.  Dostupný z <http://www.jmathlib.de/download.php>.
[20]  JmathLib site [online]. poslední revize 18.3.2011  [cit. 2011-03-18]. <http://www.jmathlib.de>.