Using Differential Evolution for Parameter Estimation in Five Dimensions Chaotic Synchronization Systems

Thanh Dung Nguyen

Tomas Bata University in Zlin,
Faculty of Applied Informatics, Nad Stranemi 4511, 76005 Zlin, Czech Republic
email: tnguyen@fai.utb.cz

Ivan Zelinka

Tomas Bata University in Zlin,
Faculty of Applied Informatics, Nad Stranemi 4511, 76005 Zlin, Czech Republic
email: ivan.zelinka@ieee.org

&
VSB-TUO Ostrava,
Department of Computer Science, 17.listopadu 15, 708 33 Ostrava-Poruba, Czech Republic

Abstract:
This paper aims to present the combination of chaotic signal and evolutionary algorithm to estimate the unknown parameters in five-dimension chaos synchronization system via the Pecora-Carroll method. The differential evolution was used to estimate the unknown parameters. Based on the results from evolutionary algorithm, two identical chaotic systems were synchronized.

Keywords:
Chaos theory, secure communication, identical synchronization, differential evolution algorithm, 5D chaotic system, Pecora-Carroll method.

Introduction

Chaos theory is one of the most important achievements in nonlinear system research. Chaos dynamics are deterministic but extremely sensitive to initial conditions. Chaotic systems and their applications to secure communications have received a great deal of attention since Pecora and Carroll proposed a method to synchronize two identical chaotic systems under different initial conditions [2]. The high unpredictability of chaotic signal is the most attractive feature of chaos based secure communication. Several types of synchronization have been considered in communication systems, such as PC method [2], OGY method [3], feedback approach [4], adaptive method [5], time-delay feedback approach [6], backstepping design technique [7], etc. In practice, some or all of the system’s parameters are unknown. So that, many of the proposed solutions focused on synchronization-based methods for parameter estimation [12]-[22]. In [21], [22], the parameters of a given dynamic model were estimated by minimizing the average synchronization error using a scalar time series, etc. However, most research about chaos synchronization concerns the synchronization of low (three-) dimensional systems. Recently, Roy and Musielak presented a five-dimensional system by adding an additional state into the three-dimensional Lorenz system [9]. Basic properties of the five-dimensional system have been analyzed by means of the Lyapunov exponents and bifurcation diagrams. Their study shows that the system can generate various complex chaotic attractors when the system parameters were changed.

Besides, differential evolution algorithm (DE) has been proposed as an alternative genetic algorithm for unconstrained continuous optimization problems. In DE system, a population of solutions is initialized randomly, which is evolved to find optimal solutions through the mutation, crossover and selection of operation procedures. It uses a simple differential operator to create new candidate solutions and one-to-one competition scheme to select a new candidate, which works with real numbers in natural manner and avoids complicated generic search for operators in GA. Therefore, DE has attracted much attention and wide applications in different fields mainly for various continuous optimization problems.

The higher dimensional systems have the more sensitive with initial conditions. The secure of communication system is increasing with the higher unpredictability of chaotic system, it also more difficult to estimate the unknown parameters.  Motivated by the aforementioned studies, this paper aims to present the combination of chaotic signal with differential evolution algorithm to estimates the unknown parameters in 5D chaotic synchronization system via Pecora and Carroll method under different initial conditions. Based on the results from DE algorithm, the estimated parameters were used to synchronize two 5D chaotic systems.

Problem formulation

Pecora-Carroll  method

In 1989, Pecora and Carroll introduced a method for constructing synchronizing chaotic systems [3].  They showed that when a state variable from a chaotic system is input into a replica subsystem of the original one, both systems can be synchronized identically. They decompose the dynamical system

(1)

into two subsystems,

(2)

with v = (u1, … , uk) and w = (uk+1, … , un). 

and considering one of the decomposed subsystems as the driving signal, say v, to be injected into the response system,

(3)

that is given by the same vector field gw, the same driving v, but different variables w´ synchronizes with the original w subsystem, i.e.

 Consider the difference of these two systems e = w´ – w. The synchronization of the pair of identical systems (2) and (3) occurs if the dynamical system describing the evolution of the difference

  .

The parameter estimation

When estimating the parameters, suppose the structure of the system is known in advance, the transmitter (driver) system is set with original parameters and the parameter in receiver (response) system is unknown. Therefore, the problem of parameter estimation can be formulated as the following optimization problem:

(4)

where M denotes length of data used for parameter estimation, the parameter can be estimated by minimum the Cost function (5).

Because of the unstable dynamic behavior of chaotic systems, the parameter estimation for chaotic systems is a multidimensional continuous optimization problem, the parameters are not easy to obtain. In addition, there are often multiple variables in the problem and multiple local optimums in the landscape of Cost function, so traditional optimization methods are easy to trap in local optima and it is difficult to achieve the global optimal parameters. Therefore, DE was chosen because it has been proven that the algorithm has the ability to converge toward the global optimum.

Differential Evolutionary Algorithms

DE is the simple yet efficient population-based evolutionary algorithm introduced by Storn and Price in 1995 [23], [24]. Over the last few years, DE has been investigated by many researches and proved very easy to be implemented with superior performance in many real optimization problems. In DE system, a population of solutions is initialized randomly, which is evolved to find optimal solutions through the mutation, crossover and selection of operation procedures. It uses a simple differential operator to create new candidate solutions and one-to-one competition scheme to select a new candidate, which works with real numbers in natural manner.

The procedure of standard DE could be described:

• Step 1: Choose control parameters: NP, F, Cr and the Generations (stopping criterion).
• Step 2: Randomly initialize the population of DE with NP individuals in the search space.
• Step 3: Evolves the system from a random initial state and obtain N sampling points of the state X at certain time points.
• Step 4: Evaluate the objective function value: first, for each individual of DE, evolves the system from the same initial state as Step 3 and obtains N sampling points of the state X at the same time points as Step 3, then calculate objective function value. Determine Xbest in current generation.
• Step 5: Perform mutation operation.
• Step 6: Perform crossover operation to obtain crossover trial vectors.
• Step 7: Calculate the objective function value of crossover trial vectors.
• Step 8: Perform selection operation to generate individual for next generation.
• Step 9: Determine the best individual of the current new generation with the best objective value. If the objective function value is better than the objective function value of Xbest, then update Xbest and its objective value with the value and objective value of the current best individual.
• Step 10: Check if the stopping criterion is met, then output Xbest; otherwise, go to Step 4.

One of the most commonly used strategy rules is Rand/1/Bin was chosen in this case 

More detailed description of DE can be found in [23], [24]

Simulation and result:

Synchronization of 5D Lorenz chaotic system

In this section, we apply the Pecora and Carroll technique to achieve the synchronization between two identical 5D chaotic systems. The mathematical description of 5D system is as follows [9]:

(5)

where x, y, z, u and w are the state variables, and a, b, c and r are the positive real constants. The 5D system (5) exhibits a chaotic attractor for a = 10, b=8/3, c = 2 and r=24.75 as shown in Fig. 1.

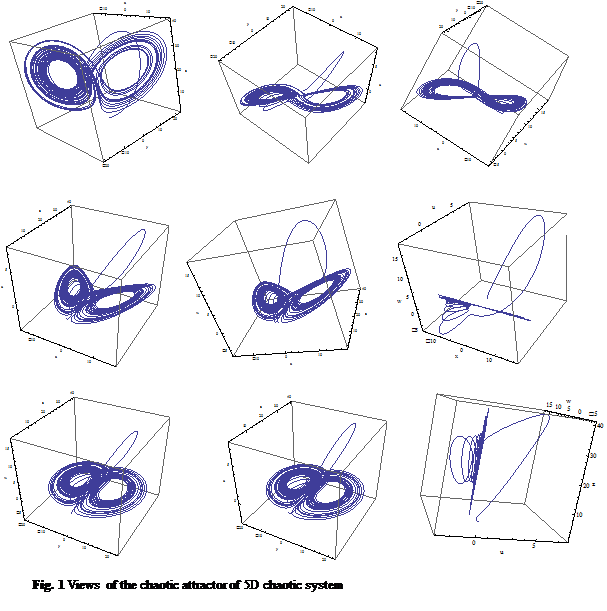In this section, we use a subscript d to denote the signals in the drive, and use a subscript r for the signals in the response. Using x of the decomposed subsystems as the driving signal, in this case, x was injected into the response system. Since xd = xr= x, we only consider the following drive and response subsystems:

(6)

And the response system Ur is described by the following equations:

(7)

where a, b, c and r are unknown parameters in response system.

Consider the difference of these two systems e = Ud – Ur The synchronization of the pair of identical systems (6) and (7) occurs if the dynamical system describing the evolution of the difference . Subtracting system (6) from system (7) yields the error dynamical system between two system e(t)= were used to create a cost function CF representing the root mean square error (RMSE) of synchronization between  Ud and Ur:

(8)

The parameter estimation can be formulated as a multidimensional nonlinear problem to minimize the cost function CF. DE are used to find a suitable parameter a, b, c and r such that the cost function CF can be asymptotical approach to minimum point. The minimum value of cost function guarantee of the best solution with suitable parameters.  Systems are asymptotically (and globally) synchronized.

Parameter setup

In our simulations, the initial states of the drive system (6) and the response system (7) are taken as xd(0) = 1, yd(0) = 2, zd(0) = 1, ud(0) = 1, wd(0) = 1  and xr(0) = 1, yr(0) =-2,  zr(0) =-1, ur(0) = -1, wr(0) = -1, respectively. Hence the error system has the initial values ex(0) = 0, ey(0) = 4, ez(0) = 2, eu(0) = 2  and ew(0) = 2. DERand/1/Bin was used to solve the systems, which the control parameters setting are given in Table1. Simulations were implemented using Mathematica programming language and executed on Pentium D 2.0G, 2GB personal computer.

Table 1: DE parameter setting

Parameter	Value
Population size NP	20
Crossover rate Cr	0.3
Mutation factor F	0.9
Generation number	100

Experimental results

In this case, we consider four-dimensional parameter estimation. That mean all of parameters a, b, c and r of response system were unknown and need to be estimated, the control parameters a,b,c and r  were known in advance with original value in driver system.

The initial guesses are in the range for a[5, 15], b[0,5], c[0,5] and r[20,30] and the control parameters of difference evolution were set as Table 1. Because of the sensitive of chaotic system, the cost function CF so complex and have a lot of local optimum. But after 80 generations, DERand/1/Bin has found the best results of CF=0.494029, the best values of the cost function approaches minimum value quickly. Both the worst and the best values of cost function approaches minimum gradually after 100 generations as shown in Fig.3. DE had found the optimum value of a,b,c and r as shown in history evolution (Fig.2), the estimated parameters have the similar value with original parameters. It can be seen that the best results (estimated values) obtained by DERand/1/Bin are almost the same and very close to the true values.

Table 2:  Estimated parameters by DE
Estimated parameter				Cost function
a	b	c	r	0.494029
9.15722	2.66624	2.04361	24.7415

In case 1,2,or 3 parameters among of a,b,c and r in response system were known in advance with the original value; the others (3,2 or 1) also were found with the optimum value by DE as show in Table 3.

Table 3:  Estimated parameters by DE
Estimated parameter				Cost function
a	9.58614			0.533740
b	2.66667			0.534798
c	2.05215			0.478855
r	24.7500			0.534798
a,b	9.59080	2.66667		0.533750
a,c	9.67232	2.05484		0.477077
a,r	9.59037	24.7500		0.533748
b,c	2.66666	2.05197		0.478994
b,r	2.66664	24.7506		0.535338
c,r	2.05217	24.7501		0.478930
a,b,c	9.79553	2.66658	2.05743	0.479627
a,b,r	9.58000	2.66667	24.7500	0.533755
a,c,r	9.57451	2.05659	24.7499	0.477361
b,c,r	2.66669	2.05119	24.7499	0.479565

After a several experiments, the estimated parameters always have the similar value with original values.  So that,   the final estimated values were chosen: a=9.15722, b=2.66624, c=2.04361 and r= 24.7415. Thus, the actual parameters were fully identified. As shown in Table.3, the values of cost function always approach to optimum values. The estimated parameters obtained by DE and original parameters have the similar values. So, it’s proven that DE is effective to estimate parameters for 5D-chaos synchronization system.

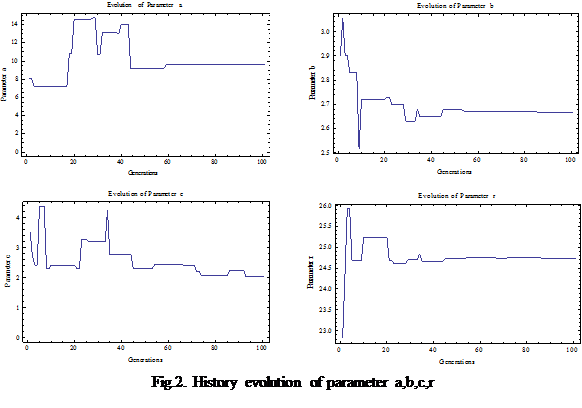
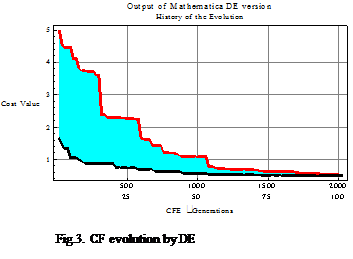
Synchronization of 5D chaotic system with estimated parameter

Base on the values were estimated by DE, the response system was constructed. The effective of the estimated value on the synchronization errors of driver systems Ud and response system Ur via PC method were demonstrated as shown in Fig. 4.

 

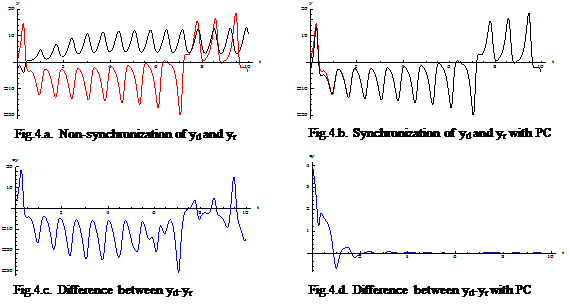
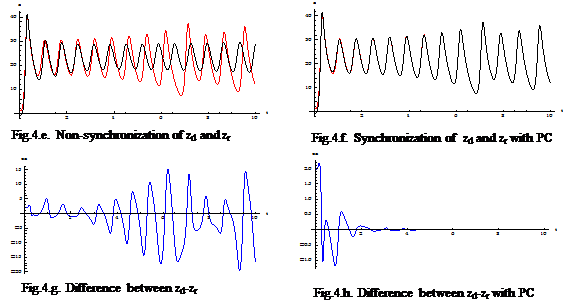
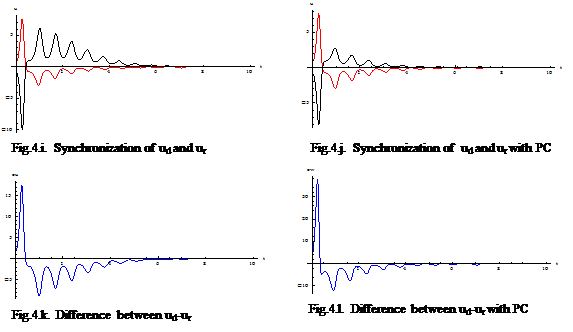
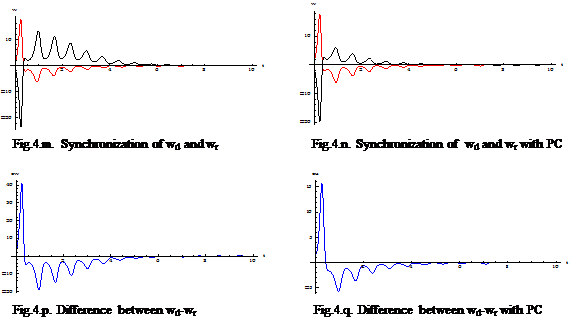
As shown in Fig.4.(a,e), the synchronization between two systems were not identified totally, and the trajectories of error e(t) were unpredicted as shown in Fig.4.(c,g). In the opposite, when PC was applied with the estimated parameters, Fig.4.(d,h) displays that the trajectories of e(t) approach to zero after t > 4 , and trajectories of yr,zr converged to yd,zd absolutely as shown in Fig.4.(b,f). It’s proven that the estimated values and PC method are effective to synchronize for two 5D-chaotic systems.

Conclusions

The main aim of this research is to show that evolutionary algorithms were used as a method of artificial intelligence to estimate parameters of chaotic synchronization systems. In this paper, we have applied the PC method to synchronize two identical 5D-chaotic systems. Parameter estimation for chaotic synchronization system was formulated as a multidimensional optimization problem. Because of the unstable dynamic behavior of chaotic systems, there is a lot of local optimum in the landscape of cost function.  Differential Evolution was used to estimate the optimum values for unknown parameters, and it easy escaped the local optimum trap and achieved the global optimum parameters. Based on the estimated parameter from DE, two chaotic systems were synchronized absolutely as demonstrated in Fig.4.

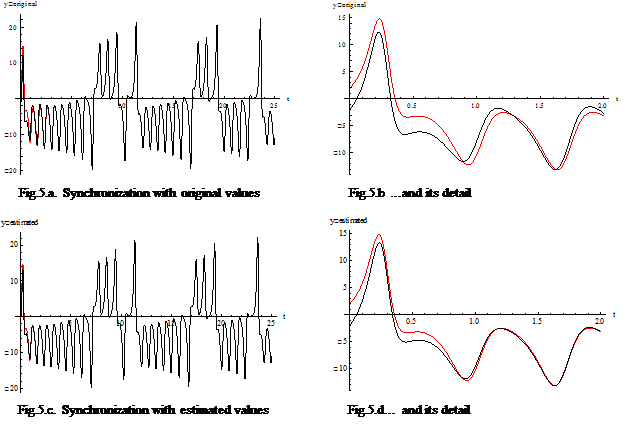
Why do we have to estimate the parameters of chaotic system when it’s have the similar the original value? Fig.5 is the answer of this question. It’s difficult to recognize what differ Fig.5.a from Fig.5.c, but in its detail as shown in Fig.5.b and Fig.5.d, the quality of synchronization with estimated parameters is clearly higher than that of original parameters. That mean the quality of communication system is increased with the estimated parameters. 

In order to improve security in chaos communication system, one would require either a much higher sensitivity of synchronization method (or more optimal of system parameters to synchronize) or a system with higher dimensionality in order to increase the number of degrees of freedom an enemy would have to scan in order to synchronize, which may happen in lower system. As the future subject, it can be extended to other synchronization method to find the more suitable, which method is much stronger of synchronization. It can also be extended to the other systems which will consider the synchronization of two difference systems or the effects of noise, fading, offset, etc. in communication system.

Acknowledgment:

This work was supported by grant No. MSM 7088352101 of the Ministry of Education of the Czech Republic and by the Grant Agency of the Czech Republic GACR 102/09/1680

References:

[1] Ivan Zelinka. Real-time deterministic chaos control by means of selected evolutionary techniques. Engineering Applications of Artificial Intelligence, 10, 2008.

[2] L. M. Pecora and T. L. Carroll. Synchronization in chaotic systems. Phys. Rev. Let., 64(8), 821–824, 1990.

[3] Ott E,Grebogi C, Yorke J A. Controlling chaos.Phys.Rev.Lett.,6411, 96-1199,1990.

[4] Chen M, Han Z. Controlling and synchronizing chaotic Genesio system via nonlinear feedback control. Chaos, Solitons and Fractals, 17709-716, 2003.

[5]  Liao Teh-lu .Adaptive Synchronization of Two Lorenz Systems, Chaos Solitons and Fractals, 9, 1555-1561. 1998.

[6] Park J H, Kwon O M. A novel criterion for delayed feedback control of time delay chaotic systems. Chaos, Solitons and Fractals, 23495-501,2005.

[7] Lü Jin-hu,Zhang Suo-chun, Controlling Chen’s chaotic attractor using backstepping design based on parameters identification. Physics Letters A,286, 148-152,2001.

[8] Nguyen T.D, Ivan Zelinka. Using method of artificial intelligence to estimate parameters of chaotic synchronization system. Mendel 2011 Soft Computing, ISSN 1803-3814. 6/2011

[9] Roy D, Musielak ZE, Generalized Lorenz models and their routes to chaos. II. Energy-conserving horizontal mode truncations. Chaos, Solitons and Fractals. 31. 747-756. 2007.

[10] Afraimovich.V.S.,Verichev.N.N.,Rabinovich,M.I., Stochastic synchronization of oscillation in dissipative systems,  Radiophysics and Quantum Electronics, Volume 29, Issue 9, pp.795-803, 1986.

[11] Kapitaniak T. Synchronization of chaos using continuous control. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. Volume 50(2):1642-1644. 1994 Aug;

[12] Shen LQ, Wang M. Robust synchronization and parameter identification on a class of uncertain chaotic systems. Chaos, Solitons & Fractals, 38, 106–111, 2008.

[13] Ge ZM, Cheng JW. Chaos synchronization and parameter identification of three time scales brushless DC motor system. Chaos, Solitons & Fractals, 24, 597–616, 2005.

[14] Li RH, Xu W, Li S. Adaptive generalized projective synchronization in different chaotic systems based on parameter identification. Phys Lett A, 367,199-206, 2007. 

[15] Guan XP, Peng HP, Li LX, Wang YQ. Parameter identification and control of Lorenz system. Acta Phys Sin, 50, 26–29, 2001.

[16] Wu XG, Hu HP, Zhang BL. Parameter estimation only from the symbolic sequences generated by chaos system. Chaos, Solitons & Fractals, 22, 359–366, 2004.

[17] Huang LL, Wang M, Feng RP. Parameters identification and adaptive synchronization of chaotic systems with unknown parameters. Phys Lett A, 342, 299–304, 2005.

[18] X. Liao, G Chen and O. wang, On Global synchronization of chaotic systems, Dynamics of continuous discrete and impulsive systems, Vol 1,2006

[19]  K. M. Cuomo and A. V. Oppenheim. Circuit implementation of synchronized chaos with applications to communications. Phys. Rev. Lett.,71(1):65–68, July 1993.

[20]  Xiaoxin Liao, Guanrong Chen and Hua O Wang. On global synchronization of chaotic systems. AK, May, 2002.

[21]  Parlitz U, Junge L. Synchronization based parameter estimation from times series. Phys Rev E, 54, 6253–9, 1996.

[22]  Parltiz U. Estimating model parameters from time series by auto synchronization. Phys Rev Lett, 76, 1232–5, 1996.

[23]   Onwubolu Godfrey and Davendra Donald. Differential Evolution: A Handbook for Global Permutation-Based Combinatorial Optimization. Studies in Computational Intelligence, Vol. 175, Springer,2009

[24]  Storn, R. and Price, K.,Differential Evolution - a Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces", Technical Report TR-95-012, ICSI, March 1995,

[25] L. Kocarev and U. Parlitz. General Approach for Chaotic Synchronization with Applications to Communication. Phys. Rev. Lett., 74, 5028–5031, 1995.

[26] M. Ding and E. Ott, Enhancing synchronism of chaotic systems, Phys. Rev. E49, R945, 1994.