Steganografie jako hrozba úniku kritických obchodních informací a její detekce pomocí umělých neuronových sítí

Jiří Hološka, Zuzana Oplatková, Ivan Zelinka, Roman Šenkeřík

Univerzita Tomáše Bati ve Zlíně, Fakulta aplikované informatiky

Nad Stráněmi 4511, Zlín 760 05

{holoska, oplatkova, zelinka, senkerik} @fai.utb.cz

Abstrakt: Tento článek se zabývá vysvětlením bezpečnostních hrozeb v byznys  prostředí, pricnipy a způsoby, jak udržovat data zabezpečená pomocí stegoanalýzy. Steganografie je doplněk kryptologie, který skrývá chráněné informace do obrázku, videí či datových toků. Steganografii je proto možné označit za ideálním nástroj k obcházení interních bezpečnostních politik omezující nežádoucí nakládání s informacemi. Článek je zaměřený na ukázku, jak lze detekovat steganografický obsah v JPEG formátu pomocí neuronových sítí (navržená metoda stegoanalýzy). Použitá metoda detekce byla ověřena s téměř 100% úspěšností, jak je popsáno v sekci výsledky.

Úvod a motivace

Následující odstavce objasňují náš zájem o steganografii zaměřenou na únik obchodních informací. V našem prvním případu si představte společnost, ve které máme databázi zákazníků umístěnou na databázovém serveru přístupnou pomocí zaměstnaneckého terminálu. Pracovník zákaznického centra obdržel nabídku od konkurence, aby ukradl informace o VIP zákaznících. Tento zaměstnanec má přístup k terminálu s monitorovaným emailovým účtem, jak je zobrazeno na Obr. 1. Pracovník uložil interní data o zákazníkovi do běžného emailu a poslal přes svůj pracovní emailový účet na svůj domácí počítač.

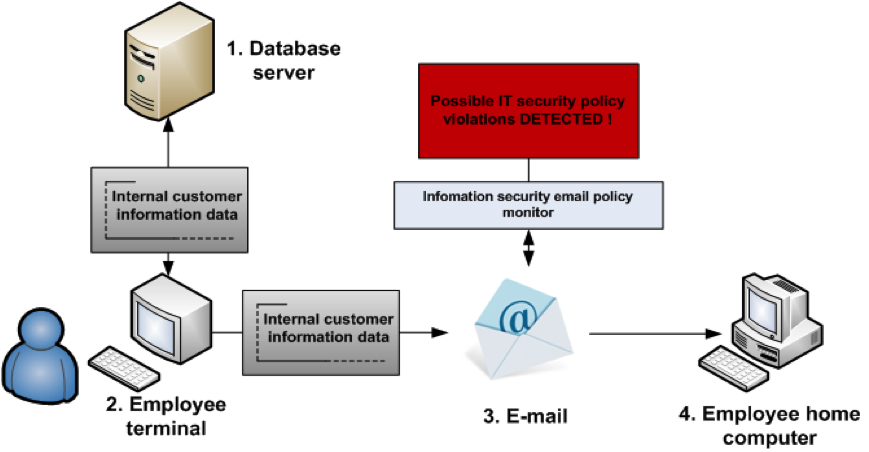
Obr. 1: Zpráva poslána běžným emailem.

Mezi zaměstnancovým terminálem a emailovou bránou je ovšem emailový scanner, který kontroluje veškerou odchozí poštu na viry a těla zpráv včetně příloh na přítomnost interních obchodních informací. V tomto případě bezpečnostní scanner detekoval, že emailová příloha obsahuje citlivé informace o VIP zákazníkovi. Bezpečnostní oddělení okamžitě dostává upozornění ohledně tohoto incidentu a zaměstnanec je následně potrestán za zneužití informací.

Obr. 2 ukazuje podobný scénář s tím rozdílem, že zde není běžný uživatel, ale uživatel se základní znalostí informačních systémů a jejich zabezpečení. Zaměstnanec není naivní a tuší, že bezpečnostní oddělení bude testovat odchozí emaily. Místo běžného emailu pošle přílohu s využitím steganografie. Pro efektivní využití steganografie je potřeba využít i kryptografie [1] - [4]. Kryptografie využívá klíčů a zprávu šifruje. Ale přesto posílání takové zprávy přitáhne pozornost lidí, kteří by o ní vědět neměli. Budou se ji snažit rozšifrovat. Steganografie umožňuje schování obsahu zprávy do multimediálních souborů, jako jsou obrázky, videa či datové toky síťových přenosů. Pokud pak vidíte takový obrázek se steganografickým obsahem, od běžného jej pouhým okem nerozeznáte (Obr. 3). A to je důvod používání steganografie.

Zaměstnanec z druhého scénáře se po zvážení možností, které má, rozhodne použít Java aplikaci staženou z internetu. Jedním důvodem je, že zaměstnanec nemá dovoleno instalovat jakékoliv aplikace na svůj terminál. Druhým důvodem je, že Java aplikace jsou multiplatformní, tj. je možné je provozovat na MS Windows stejně dobře jako na Unixových či podobných systémech.

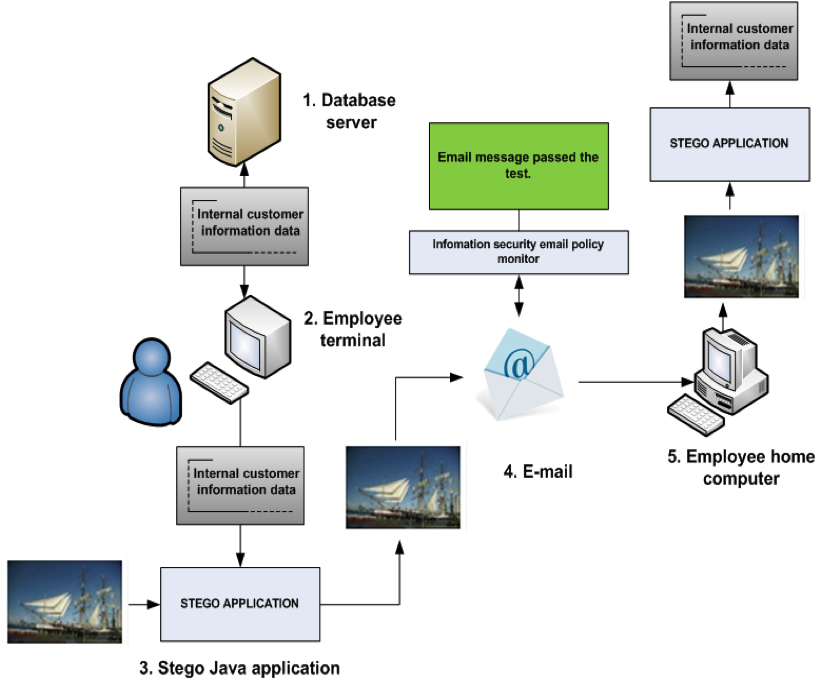
Obr. 2: Zpráva odeslaná se steganografickým obsahem.

a)

b)

Obr. 3: Příklady a) čistého a b) stego obrázku.

Celý scénář je velmi jednoduchý. Zaměstnanec si připraví několik obrázků v JPEG formátu a steganografickou Java aplikaci. Následně vloží textový soubor obsahující interní obchodní informace do připravených JPEG obrázků. A tyto obrázky si pošle emailem na svůj domácí emailový účet.

Náš zkorumpovaný zaměstnanec může použít ještě důmyslnější scénář. Založí si nový emailový účet na jakémkoliv veřejném emailovém serveru. Napíše si odsud do práce emailovou zprávu s textem typu: „Nazdar Bobe, posílám ti pár fotek z prázdnin, jak jsi je minulý týden chtěl. Měj se hezky. Marek.“ K tomuto emailu přiloží obrázky a steganografickou aplikaci. Druhý den v práci najde tuto zprávu a odpoví na ni např.: „Ahoj Marku, věřím, že jsi spletl emailovou adresu příjemce, protože toto adresa zákaznického servisu firmy XY. Prosím, zkontroluj si adresu příjemce a pošli to znovu. Měj se fajn. Tom. P.S. Jsem si jistý, že se Bobovi budou fotky líbit.“ Samozřejmě ke zprávě přiloží obrázky s vloženými informacemi o zákazníkovi jako v předcházejícím případě. A pošle. Tuto zprávu v systému zákaznické podpory označí jako nesprávně doručenou, zaměstnanec tím od sebe odkloní pozornost a citlivé informace bezpečně vynese z firmy.

Proto je důležité mít kvalitní metodu pro sledování a detekci stegoprogramů, aby se co nejvíce eliminovala možnost zneužití steganografie. Tento článek se zabývá právě detekcí steganografie pomocí umělých neuronových sítí. Je zaměřený na detekci obrázků, do kterých byla informace vložena programem CipherAWT využívající algoritmus F5. Nejprve se budeme zabývat samotným algoritmem a programem CipherAWT, dále bude vysvětlena extrakce dat z JPEG obrázku a jejich transformace do trénovací množiny pro neuronové sítě. Jejich popis je pak v dalším odstavci a je následován sekcí o výsledcích. Není zde řešeno samotné dešifrování zprávy, ale pouze detekce steganografického obsahu v obrázcích.

Steganografické nástroje

Nyní je známo velké množství steganografických nástrojů, většinou se jedná o opensource implementace. Některé jsou v popředí našeho zájmu a tohoto výzkumu, např. OutGuess, Steghide, F5 a další [5]. Tento článek je zaměřený na detekci obrázků kódovaných algoritmem F5. Následující část je pak zaměřena popis F5 algoritmu a jeho implementace v programu CipherAWT.

F5

Steganografický algoritmus F5 byl představen německými výzkumníky Pfitzmannem a Westfeldem v roce 2001 [6]. Cílem jejich projektu bylo vyvinout koncept a praktickou metodu ukrývání pro JPEG obrázky, který by poskytoval vysokou steganografickou kapacitu bez ztráty bezpečnosti. Vedeni ?2 statistickým útokem zpochybnili paradigma nahrazování bitů informace v čistém obrázku tajnou zprávou, zatímco předkládají jiné paradigma načítání obrazových komponent k ukrytí bitů zprávy. Místo nahrazování LSB (nejméně významných bitů) kvantizovaných DCT (diskrétní kosinové transformace) koeficientů bity zprávy, absolutní hodnota koeficientů je snížena o jedničku. Autoři tvrdí, že tento typ ukrývání nemůže být detekovaný použitím statistického útoku ?2. Algoritmus F5 ukrývá bity zprávy do náhodně vybraných DCT koeficientů a vkládání informací se optimalizuje pomocí matice, která slouží se snížení nezbytného počtu změn k ukrytí zprávy určité délky [7].

CipherAWT

CipherAWT, verze 13.0.0, byl napsán Andreasem Westfeldem jako Java implementace F5 algoritmu. Tento nástroj má grafické uživatelské prostředí. Z tohoto důvodu je velmi jednoduchý k použití. Další výhodou je možnost použití na více platformách stejně jako mnoho dalších Java aplikací. Pokud na počítači je nainstalovaný doplněk Java Runtime Environment, Cipher AWT pak může běžet na MS Windows, Linux nebo Mac OS X [7].

Detekce

Nejprve je důležité získat data pro trénovací množiny v neuronových sítích. Pro tento účel jsme použili tabulky Huffmanova kódovaní z JPEG obrázků.

Huffmanovo kódování

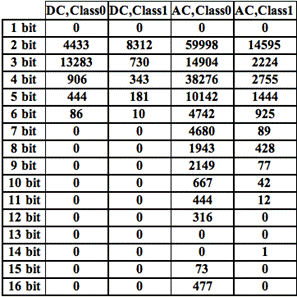
Huffmanovo kódování bylo navrženo Davidem Huffmanem v roce 1952. Tato metoda bere symboly, v tomto případě hodnoty diskrétní kosinové transformace (jedna z metod, jak prezentovat informace v obrázcích typu barva, sytost, jas...) a transformuje je do kódu proměnné délky. Toto je uděláno tak, že podle statistiky, nejkratší bitová reprezentace je použita pro symboly s nejčastějším výskytem. Huffmanovo kódování má dvě velmi důležité vlastnosti — je to kód s minimální délkou a prefixový kód, tj. může být dekódován jednoznačně. Na druhou stranu je zde i nevýhoda, výskyt každého symbolu musí být znám a priori. Ale v případě obrázků se pracuje s odhadem, který se upravuje během komprese [8]. Obr. 4, Obr. 5 a Tab. 1 ukazují rozdíl mezi čistým a stego obrázkem ve stejnosměrné a střídavé složce (DC a AC). Na grafech je pak vynesen počet jednotlivých bitových slov vyskytujících se v obrázku.

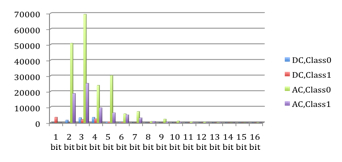
Obr. 4: Graf histogramu Huffmanova kódování— čistý obrázek

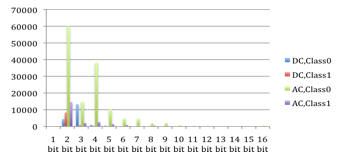
Obr. 5: Graf histogramu Huffmanova kódování— stego obrázek (se skrytou informací)

Tab. 1: Histogram Huffmanova kódování— a) čistý obrázek, b) stego obrázek

a)

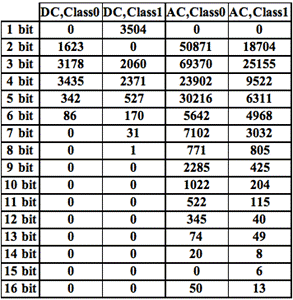
b)

Pro představu, jaký vliv má steganografie na nosné obrázky JPEG v formátu, je možné se podívat na následující dva obrázky (Obr. 6 a) a b)). Každé bitové slovo si lze představit jako cihlu ve stěně. Z cihel je možné postavit dvě stejně velké zdi, ale v obou případech budou postaveny z různých cihel. Tyto dvě zdi budou sice stejně velké, ale mají různou strukturu (různý výskyt cihel a některé cihly se také objevují častěji než jiné). Analogicky je možno se dívat na „nosné“ a „stego“ obrázky. Jsou stejně velké, ale struktura je jiná — jiná délka bitového slova a také jiný počet bitových slov.

a)

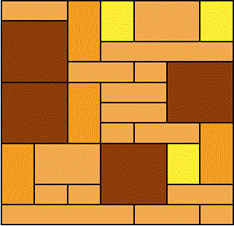
b)

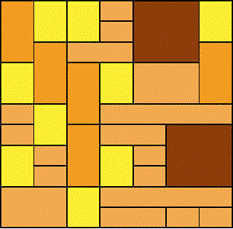
Obr. 6: Ilustrace Huffmanova kódování— a) čistý obrázek, b) stego obrázek

Jelikož je cílem steganografie neupozorňovat na sebe, stego obrázky proto musí vypadat jako bežné obrázky z digitálních fotoaparátů. Vizuálně se tedy jedná o identické obrázky, nastěstí se liší vnitřní datovou strukturou. Tyto rozdíly jsou natolik velké, že mohou být použity pro správné naučení umělé neuronové sítě.

Jak tedy trénovací množiny vypadají? Pro každý případ bylo vzato všech 64 čísel z Huffmanova kódování (16 bitových slov pro dvě třídy stejnosměrné i střídavé složky), viz. Obr. 7 a Obr. 8.

{{0,2181,49638,11923,7754,3614,2113,1328,181,0,0,0,0,0,0,0,0,37838,17016,9603,6323,4489,2770,
691,2,0,0,0,0,0,0,0,0,1184544,266832,407253,225804,86439,84594,39260,27220,14603,6757,1326,
0,0,57,5077,0,294505,156163,135414,76507,49051,12597,16388,9120,3521,1513,93,0,881,629,86},

Obr. 7: Příklad trénovací množiny jednoho prvku (obrázku) pro nosné obrázky

{{0,2178,49642,11918,7758,3614,2113,1328,181,0,0,0,0,0,0,0,0,37824,17026,9608,6323,4486,2771,
692,2,0,0,0,0,0,0,0,0,1184565,266816,406818,225770,85887,84320,39638,27400,14811,6889,1516,
0,0,105,5231,0,295156,155514,135282,76214,48989,12495,16659,9154,3609,1601,94,0,868,625,208},

Obr. 8: Příklad trénovací množiny jednoho prvku (obrázku) pro stego obrázky

Umělé neuronové sítě

Umělé neuronové sítě jsou nástroje umělé inteligence, které byly vyvinuty v první polovině 40. let 20. století. Po publikování Pittsova — McCullochova modelu [9] neuronu (Obr. 9) a Rosenblattovy první neuronové sítě Perceptron s učícím algoritmem Minsky a Papert způsobili opuštění výzkumu neuronových sítí na nějaký čas. Percetpron totiž nebyl schopný řešit nelineárně separabilní problémy. Naštěstí v 80. letech se vědci vrátili, protože byl podán důkaz, že neuronové sítě jsou schopné takového řešení, a tím byl odstartován boom výzkumu neuronových sítí [10].

 

.

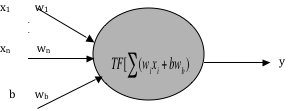Obr. 9: Model neuronu — TF (přenosová funkce), x₁ - x_n (vstupy do neuronové sítě), b — práh, w₁ — w_n, w_b — váhy, y — výstup

Umělé neuronové sítě (NN) byly inspirovány biologickými neuronovými sítěmi a jsou používány pro komplexní a těžké úlohy. Nejčastější použití je klasifikace objektů, protože NN jsou schopné zobecňování, a tak je klasifikace pro ně přirozená. Další možnosti jsou např. rozpoznávání vzorů, řízení, filtrace signálů a také aproximace dat. Klasifikace je vlastnost, kterou je zde použita.

Simulace byly provedeny se sítí s dopředným šířením signálu s učením. NN potřebuje trénovací množinu známých řešení, aby se na nich mohla dobře naučit. Neuronová síť pracuje tak, že vstupy musí být převedeny na čísla vhodným způsobem. Tyto vstupy jsou pak násobeny váhami a přes přenosovou funkci je získán výstup. Přenosové funkce jsou např. logistická sigmoida, lineární funkce, hyperbolický tangens apod.

Neuronové jednotky (Obr. 9) jsou spojovány přes různé struktury do sítí (např. Obr. 10), jako jsou s jednou či více vrstvami, úplným propojením či jiným typem. Tyto sítě jsou pak navrženy pro různé úlohy. Sítě s dopředným šířením signálu mají různé typy učících algoritmů — nejvíce známý Backpropagation, Pruningův algoritmus, gradientní metody, Levenberg-Marquardtův algoritmus [11]. V posledních letech se také používají různé evoluční algoritmy pro učení, jako jsou genetické algoritmy, Diferenciální evoluce [12], apod. V publikovaných simulacích byl použit Levenberg-Marquardtův algoritmus. V budoucnu ale předpokládáme také použití evolučních algoritmů jako je SOMA [13] či Diferenciální evoluce, protože klasifikace konkrétních stego programů nebude pravděpodobně jednoduchý optimalizační případ pro správné nalezení vah v neuronové síti.

A)

B)

Obr. 10: Model neuronových sítí— A) s jednou skrytou vrstvou a jedním výstupem, B) dvě skryté vrstvy a více výstupů, kde a . Tyto obrázky jsou převzaty z toolboxu Neural Networks pro software Mathematica (www.wolfram.com), protože tento nástroj byl použitý v průběhu simulací. Také jména byla převzata z tohoto prostředí kvůli spekulacím, co to znamená.

Nastavení pro simulace

Během simulací byla použita jedna skrytá vrstva s 8 neurony ve skryté vrstvě a lineární omezenou funkcí. Výstupní funkcí je logistická sigmoida. Počet iterací byl nastaven na 50. Zkoušeli jsme také síť se dvěma skrytými vrstvami, kde bylo 16 a 4 neurony. Typ funkcí jako v prvním případě. Ale zde platilo pravidlo, jednodušší nastavení vyhrává. Síť se dvěma skrytými vrstvami nebyla tak úspěšná jako ta s jednou skrytou vrstvou. Následující graf je příklad učícího procesu s trénovací chybou téměř nulovou, úspěšné učení (Obr. 11).

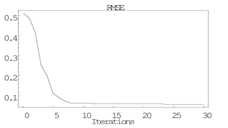
Obr. 11: Globální chyba při učení jednovrstvé neuronové sítě — RMSE

Výsledky

Pro trénování bylo použito celkem 18000 vzorků (10 800 čistých obrázků, 7200 F5 stego obrázků). Bylo provedeno 30 iterací při učení. Testovalo se celkem 6777 obrázků (4068 čistých, 2709 F5 stego). Následující tabulka (Tab. 1) ukazuje výsledky pro testování čistých a F5 stego obrázků. Tab. 3 pak ukazuje testování i ostatními stego programy, které jsme zatím použili (OutGuess, Steghide [5]). Pro tento případ bylo použito samozřejmě nové učení a nové testování. Proto se zde objevují jiná čísla, než v prvním případě. Z čísel je jasně patrné, že neuronové sítě jsou schopné této aplikace, je zde 100% úspěšnost.

Tab. 2: Výsledky detekce pro síť s jednou skrytou — A —Počet špatně zařazených případů (chyby) z x, B — procentuální chybovost, C — procentuální úspěšnost (100 — procentuální chybovost)

	A	B	C
Čisté obrázky (x=4 068)	22	0.54	99.46
F5 stego obrázky (x=2 709)	0	0	100

Tab. 3: Výsledky detekce pro síť s jednou skrytou a více programů — A —Počet špatně zařazených případů (chyby) z x, B — procentuální chybovost, C — procentuální úspěšnost (100 — procentuální chybovost)

	A	B	C
Čisté obrázky (x=4 068)	0	0	100
F5 stego obrázky (x=2 709)	0	0	100
Steghide stego obrázky (x = 9 933)	0	0	100
OutGuess stego obrázky (x = 3 644)	0	0	100

Závěr

Tento článek se zabývá detekcí steganografického obsahu v obrázcích vložených programem CipherAWT (F5 algoritmus). Detekce byla provedena pomocí neuronové sítě s dopředným šířením signálu (feedforward artificial neural network) s jednou skrytou vrstvou. Tato síť byla úspěšná téměř ve 100 % všech klasifikovaných případů — 6777 testovacích obrázků. Také RMSE (odmocnia průměrné hodnoty druhých mocnin), která se používá pro měření globální chyby u neuronových sítí, se blížila nule, tj. učení neuronové sítě bylo úspěšné. Cílem tohoto výzkumu je vyvinout univerzální detektor stego programů, samotný detektor může být implementován jako modul poštovních serverů, který bude kontrolovat, zda se v odchozí poště nenacházejí důvěrné informace. Tento detektor bude pouze vyhledávat steganogramy, nebude se tudíž zabývat dešifrováním zprávy jako takové, ale jen o odkrytí její existence. Budoucí práce předpokládá učení dalších typů neuronových sítí a také učení na dalších stego aplikacích, aby se potvrdila možnost adaptace neuronových sítí na tento typ problémů. Současná práce v tomto výzkumu je také zaměřena na datamining, aby se snížil počet neuronů, vah či vstupních uzlů.

Poděkování

Tato práce byla podporována grantem č. MSM 7088352101 Ministerstva školství České Republiky a grantem Grantové agentury České Republiky č. 102/09/1680.

Literatura

• [1] Radcliff D.: Steganography: Hidden Data, June 10, 2002, http://www.computerworld.com/securitytopics/security/story/0,10801,71726,00.html

• [2] Bailey K., Curran K.: Steganography, BookSurge Publishing, 2005, ISBN: 159457667X

• [3] Steganography, cited 2008-03-20, http://en.wikipedia.org/wiki/Steganography

• [4] Wayner P.: Disappearing Cryptography, Morgan Kaufmann, 2002, ISBN: 1558607692

• [5] Oplatkova Z., Holoska J., Zelinka I., Senkerik R.: Detection of Steganography Content Inserted by Steghide by means of Neural Networks, Mendel 2008, ISBN: 978-80-214-3675-6

• [6] Fridrich, J., Goljan, M., and Hogea, D. "Steganalysis of JPEG Images: Breaking the F5 Algorithm." 5th Information Hiding Workshop, Noordwijkerhout, The Netherlands, Oct. 2002. URL: http://www.ws.binghamton.edu/fridrich/Research/f5.pdf. Last accessed: 2003-12-24.

• [7] Westfeld, A.: High Capacity Despite Better Steganalysis (F5—A Steganographic Algorithm). In: Moskowitz, I.S. (eds.): Information Hiding. 4th International Workshop. Lecture Notes in Computer Science, Vol.2137. Springer-Verlag, Berlin

• [8] Benes M.: Komprese: Huffmanovo kódování, cited 2008-02-15, http://www.cs.vsb.cz/benes/vyuka/pte/texty/komprese/ch02s02.html

• [9] McCulloch W. S., Pitts W. A logical calculus of ideas immanent in nervous activity, In Bulletin of Mathematical Biophysics, 5:115, 133, 1943
• [10] Hertz J., Kogh A. and Palmer R. G. Introduction to the Theory of Neural Computation, Addison — Wesley 1991
• [11] Reitermanova Z. Feedforward Neural Networks — Architecture Optimization and Knowledge Extraction, WDS'08 Proceedings of Contributed Papers, Part I, 159—164, 2008, MATFYZPRESS, ISBN 978-80-7378-065-4
• [12] Lampinen J., Zelinka I., New Ideas in Optimization — Mechanical Engineering Design Optimization by Differential Evolution. Volume 1. London: McGraw-Hill, 1999. 20 p. ISBN 007-709506-5
• [13] Zelinka I. 2004a, „SOMA — Self Organizing Migrating Algorithm“, In: B.V. Babu, G. Onwubolu (eds), ), New Optimization Techniques in Engineering Springer-Verlag, 2004, ISBN 3-540-20167X