Simple robust controllers for systems with time delay using direct search methods

Simple robust controllers for systems with time delay using direct search methods

Marek Dlapa
Department of Automation and Control Engineering
Faculty of Applied Informatics
Tomas Bata University in Zlin, Czech Republic

e-mail: dlapa@ft.utb.cz

Abstrakt: V tomto článku bude odvozen postup návrhu jednoduchých regulátorů pro jednorozměrové systémy. Vlastní regulátor je získán optimalizací pólů nominálního zpětnovazebního obvodu za využití strukturovaného singulárního čísla označovaného jako μ-funkce, která zohledňuje podmínky robustní kvality a stability řídícího obvodu. Regulátor je řešením diofantické rovnice v okruhu racionálních ryzích a stabilních funkcí. Jako optimalizační nástroj je použit evoluční algoritmus diferenciální migrace, který je schopen nalézat řešení pro hodnotící funkce s mnoha lokálními extrémy. Finální regulátor je porovnán s D-K iterací jako standardní metodou pro μ‑syntézu.

Introduction

Many important results have been derived in the field of robust control theory during recent decades. The algebraic theory developed by Kučera (1972) for discrete and Vidyasagar (1985) for continuous time systems bringing simple procedures for controller design. On the other hand, there was an increased research activity focused on structured and unstructured uncertainties with dynamic perturbations (Doyle, 1982; 1985; Doyle et al., 1982; 1992) resulting in tools that can assess both robust stability and performance of systems with mixed structured uncertainty. The main result is the structured singular value denoted μ making possible analysis of mixed structured uncertainties in case they can be treated via the linear fractional transformation (LFT). A common method for μ‑synthesis is the D‑K iteration using the upper bound of μ together with formulae for the H_¥ (sub)optimal controller derived by Doyle et al. (1989) and Gahinet and Apkarian (1994).

The methods for μ‑synthesis are well known but still there are some difficulties that need to be resolved. Particularly the fact that the D‑K iteration does not guarantee convergence to the global or even local minimum leading to non‑optimality of the resulting controller (Stein and Doyle, 1991). Another issue follows from high order of the resulting controllers. Such controllers are usually simplified through approximation by a low order system causing deterioration of the closed loop frequency characteristics.

In this paper, an approach solving the problem of convergence to the global minimum is presented yielding controllers with PI and PID structure. The method introduces an algebraic procedure securing that the poles of the nominal closed loop system are constrained to the left half‑plane. The cost function is defined as supremum of the μ‑function upper bound in the frequency domain. In order to overcome the problem of multimodality of the cost function evolutionary algorithm Differential Migration is used.

The first step in the design is finding all solutions to Diophantine equations in the ring of Hurwitz-stable and proper rational functions (R_ps). The controllers are functions of nominal closed-loop poles, which are the tuning parameters. Then the search of the optimal pole placement is performed via the Differential Migration [DM, see Dlapa and Prokop (2008), Dlapa (2009)] algorithm and the rough results are tuned up by the Nelder-Mead simplex method moving the poles to the local minimum. Robust stability and performance is verified by checking the supremum of the μ‑function upper bound in the frequency domain. The other specifications are guaranteed by divisibility in R_ps and the choice of performance weighting function.

Finally, it is shown that, in some cases, tuning the controller by a scalar parameter equal to nominal closed-loop poles being in one point is not satisfactory for finding a stabilizing solution.

Algebraic design

Assume a feedback system with two exogenous inputs r and d depicted in Figure 1. Here e = r — y is the tracking error, r is the reference and d is a disturbance. Consider a plant defined by transfer function

       (1)

which can be rewritten in terms of its coefficients and transformed to the elements of R_PS

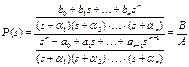, A, B Î R_PS    (2)

The controller K = N/M is obtained by solving the Diophantine equation

AM + BN = 1  (3)

with A, B, M, N Î R_ps. The Diophantine equation (3) is often called the Bezout identity. All feedback controllers N/M are given by

, (4)

where , are particular solutions of (3) and T is an arbitrary element of R_PS.

The controller K satisfying equation (3) guarantees the BIBO (bounded input bounded output) stability of the feedback loop in Figure 1 (Kučera, 1984; Morari and Zafiriou, 1989; Vidyasagar, 1985). This is a crucial point for the theorems regarding the structured singular value. If the BIBO stability is held, then the nominal model is internally stable and theorems related to robust stability and performance can be used.

 

Figure 1 Feedback system

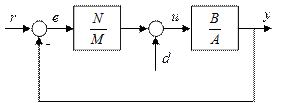It can be shown that the asymptotic tracking of reference signal is achieved if and only if AM is divisible by F_r and disturbance is suppressed if AM is divisible by F_d, where F_r and F_d are denominators of Laplace transforms of the reference and disturbance, respectively.

Structured singular value

Define D as a set of block diagonal matrices

    (5)

where S is the number of repeated scalar blocks,

                        F is the number of full blocks,

            r₁,¼, r_S and m₁,¼, m_F are positive integers defining dimensions of scalar and full blocks.

For consistency among all the dimensions, the following condition must be held

            (6)

Definition 1: For M Î C^n´n is μ_D(M) defined as

         (7)

If no such D Î D exists making I — MD singular, then μ_D(M) = 0.

Consider a complex matrix M partitioned as

          (8)

and suppose there is a defined block structure D₂ which is compatible in size with M₂₂ (for any D₂ Î D₂, M₂₂D₂ is square). For D₂ Î D₂, consider the following loop equations

e = M₁₁d + M₁₂w

z = M₂₁d + M₂₂w         (9)

w = D₂z

If the inverse to I — M₂₂D₂ exists, then e and d must satisfy e = F_L(M, D₂)d, where

F_L(M, D₂) = M₁₁ + M₁₂D₂(I — M₂₂D₂)^—1M₂₁     (10)

is a linear fractional transformation on M by D₂, and in a feedback diagram appears as the loop in Figure 2.

The subscript L on F_L pertains to the lower loop of M and is closed by D₂. An analogous formula describes F_U(M, D₁), which is the resulting matrix obtained by closing the upper loop of M with a matrix D₁ Î D₁.

 

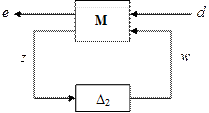Figure 2. LFT interconnection.

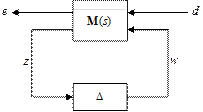
Assume M is a stable, real-rational, proper transfer function matrix, with n_z + n_d inputs, and n_w + n_e outputs. Partition M in the obvious manner, so that M₁₁ has n_z inputs and n_w outputs, etc. Define a block structure

         (11)

The setup is to address theoretically the robust performance about the loop shown in Figure 3. The perturbed function from d to e is denoted F_L(M, D).

Theorem 1 (Doyle et al., 1982): Let b > 0. For all D(s) Î D with , the loop shown in Figure 3 is well-posed, internally stable, and if and only if

       (12)

            ■

 

Figure 3 Robust performance

System with uncertain time delay

Time delay systems are one of the main areas of robust control applications. Such systems are difficult to control by means of standard methods even if the parameters are constant. If time delay varies then the problems related with control are severe. The set of plants considered in this paper has uncertain time delay, which is ten times longer than the dynamics constants. The system is not easy to control in the framework of linear time invariant systems even if the time delay is approximated by Taylor series.

The plant family is defined as follows:

       (13)

The control objective is to find a controller that guarantees the robust stability and performance for every plant from the set P. The time delay is treated by multiplicative uncertainty

    (14)

Let the nominal plant be

    (15)

then for the weighting function W₂ the following inequality must be held

, ,            (16)

which is equivalent to

, , (17)

The weight W₂ is an envelope curve of for τ = 10 (see Figure 5):

  (18)

Define sensitivity function as transfer function from reference r to error e in Figure 4 with P Î P:

       (19)

Then the performance condition is of the form:

||W₁S||_¥ £ 1      (20)

 

Figure 4. Feedback loop

In order to obtain asymptotic tracking of stepwise reference signal weight W₁ is defined as:

    (21)

 

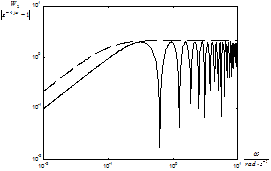Figure 5 Bode plot of W₂ and

Multiplicative uncertainty (14) and performance condition exactly fit the LFT framework. The closed‑loop interconnection for the μ‑synthesis is in Figure 6. Here W_n represents the sensor noise weighting function and K is the controller. The weight

          (22)

is a high pass filter reflecting the properties of the noise arising in sensors.

Generalized plant G can be partitioned to

            (23)

The block structure of G corresponds with the input and output variables in Figure 6:

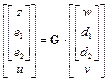        (24)

The design objective is to find a stabilizing controller K such that

            (25)

is minimal where

          (26)

is the lower linear fractional transformation on generalized plant G and controller K (see Figure 6).

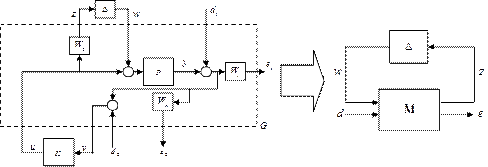
Figure 6 Closed-loop interconnection for μ‑synthesis

Transfer matrix M can be partitioned to

          (27)

The relationship between inputs and outputs is as follows

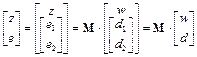          (28)

Then the transfer function from d to e is the upper linear fractional transformation on M and D

    (29)

Perturbation in Figure 6 is a diagonal matrix

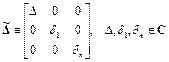     (30)

For performance and stability the following corollary of Theorem 1 holds.

Corollary 1: The closed loop in Figure 6 is internally stable for all D, |D| < 1, D Î C and if and only if

        (31)

for all frequencies.

            ■

For the particular example Corollary 1 can be modified as follows:

Corollary 2: The closed loop in Figure 4 is internally stable for all P Î P and performance condition (20) holds if and only if

        (32)

for all frequencies.

            ■

Hence, the structured singular value being lower than one indicates that the closed loop in Figure 4 is internally stable and performance condition (20) holds for all plants from the set P.

Algebraic Approach

The controller is obtained by solving the Diophantine equation (3). The degrees of M and N are chosen so that the number of closed loop poles is minimal and the asymptotic tracking for stepwise reference signal is achieved:

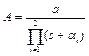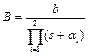, (32)

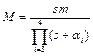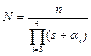,            (33)

Hence degrees of polynomials m, n are:

∂m = 1, ∂n = 2            (34)

The resulting controller has the PID structure:

     (35)

Optimization using the Differential Migration with subsequent tuning by the Nelder-Mead simplex method gave the resulting poles:

   (36)

and the controller

       (37)

Relationship with other algebraic methodologies

Some authors make all nominal closed loop poles equal to a scalar parameter and the parameter is used for tuning (Prokop and Corriou, 1997). However, if the nominal plant is defined by (15) then there is no stabilizing controller. In Figure 7 the dependence of the crossing of the open loop transfer function L with real axis on the tuning parameter m is depicted. The Figure proves that there is no multiple closed loop pole m such that Nyquist plot of L crosses the interval (-1, 0) on the real axis.

 

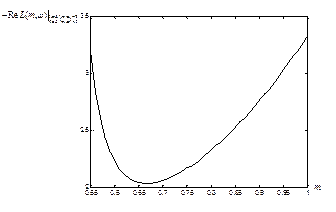Figure 7 Proof of absence of a stabilizing controller for multiple nominal closed loop poles

A stabilizing controller exists only if the time delay is approximated by Taylor series in the numerator of the nominal plant. Define the nominal plant as

         (38)

and the perturbed plant

         (39)

Then a controller stabilizing the closed loop in Figure 4 exists for m = 0.4:

      (40)

Simulations

The D-K iteration is used as a reference, which is a common method for μ‑synthesis. Weight W₁ is modified so that conditions for DGKF formulae are held (Doyle et al., 1989):

          (41)

The controller obtained from the D‑K iteration has 25 states. Such controller is too complex for real world applications and it is desirable to approximate it by a low order transfer function. However, if the simplification is too substantial then the frequency characteristics of the resulting controllers degrade as shown in Figure 8. For the 3^rd order controller the peak of the μ‑function is higher than 1 and the robust stability and performance is not guaranteed.

Approximation by a low order transfer function gave the following controller:

           (42)

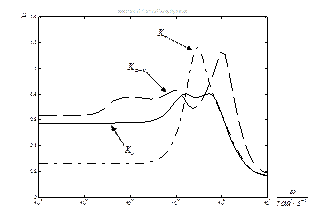
The controller with nominal closed loop poles equal to a scalar parameter has the highest peak of the μ‑plot, which does not guarantee that the robust stability and performance conditions are held (Figure 10). Similar results were obtained via the D‑K iteration with μ‑function higher than one. Algebraic approach with evolutionary optimization yields the peak of the μ‑function lower than one implying that the robust stability and performance conditions are held. The controllers were verified by simulations with the closed-loop interconnection depicted in Figure 9, where K = K_m, K_D‑K and K_A. Algebraic μ‑synthesis has faster tracking than the D‑K iteration and monotonous response to stepwise reference signal (see Figures 11 to 13). Controller K_m has an overshoot, which decreases with decreasing time delay. Sensor noise has almost no influence on the output quantity (Figure 13). Sensor noise used in simulation was the white noise whose spectral density was shaped by the following high pass filter:

         (43)

The noise used for simulation is depicted in Figure 14. It is a high frequency noise typically arising in sensors.

 

Figure 8 Degradation of the frequency characteristics during simplification process

 

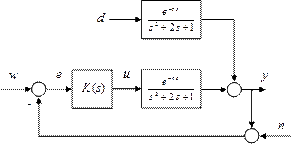Figure 9 Feedback system used for simulation

 

Figure 10 μ‑plot comparison

 

Figure 11 Simulation of response to stepwise reference signal for τ = 10, controller K_m (dash-dotted), K_D‑K (dashed) and K_A (solid)

 

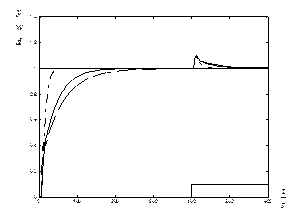Figure 12 Simulation of response to stepwise reference signal for τ = 5, controller K_m (dash-dotted), K_D‑K (dashed) and K_A (solid)

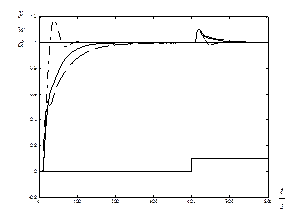
Figure 13 Simulation of response to stepwise reference signal for τ = 10, controller K_m (dash-dotted), K_D‑K (dashed) and K_A (solid) subject to sensor noise

 

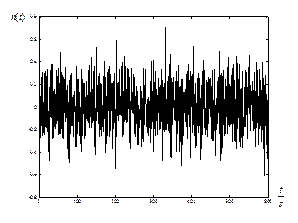Figure 14 Sensor noise at the input to the controller

Conclusion

The paper has shown a design of simple robust controllers via structured singular value using algebraic approach. In the design procedure, the controller was obtained via minimization of supremum of the μ‑function and the nominal closed loop poles were used as the tuning parameters. The robust stability and performance conditions are held due to the properties of appropriate μ‑plots being lower than one and to the fact that the nominal closed loop poles are constrained to the left half-plane providing stability of the generalized plant. The example of time delay system control demonstrates faster set-point tracking and a monotonous response to stepwise reference signal of the proposed methodology, which is not true for the D‑K iteration and common algebraic synthesis.

Acknowledgment

This work was supported by the Ministry of Education Youth and Sports of the Czech Republic under Grant MSM7088352102.

References

• Dlapa, M. and Prokop, R. (2008) Design and analysis of simple robust controllers via structured singular value, Int. J. Automation and Control, Vol. 2, No. 1, pp. 73-89, ISSN (Online) 1740-7524, ISSN (Print) 1740-7516.
• Dlapa, M. (2009) Differential Migration: Sensitivity Analysis and Comparison Study, In 2009 IEEE Congress on Evolutionary Computation (IEEE CEC 2009), pp. 1729-1736, ISBN 978-1-4244-2959-2.
• Doyle, J.C. (1982) ‘Analysis of feedback systems with structured uncertainties’, Proceedings of IEEE, Part-D, 129, pp. 242-250.
• Doyle, J.C, Wall, J. and Stein, G. (1982) ‘Performance and robustness analysis for structured uncertainty’, Proceedings of the 21st IEEE Conference on Decision and Control, pp. 629-636.
• Doyle, J.C. (1985) ‘Structure uncertainty in control system design’, Proceedings of 24th IEEE Conference on Decision and Control, pp. 260-265.
• Doyle, J.C., Glover, K., Khargonekar, P.P. and Francis, B.A. (1989) ‘State-space solutions to standard H₂ and H_∞ control problems’, IEEE Transactions on Automatic Control, Vol. 34, No. 8, pp. 831-847.
• Doyle, J.C., Francis, B.A. and Tannenbaum, A.R. (1992) Feedback control theory, Macmillan Publishing Company, N.Y.
• Gahinet, P. and Apkarian, P. (1994) ‘A linear matrix inequality approach to H_¥ control’, International Journal of Robust and Nonlinear Control, Vol. 4, pp. 421-449.
• Kučera, V. (1972) Discrete Linear Control: The Polynomial Equation Approach, Wiley, New York.
• Kučera, V. (1979) Discrete Linear Control, Wiley, Chichester, U.K.
• Kučera, V. (1984) ‘Design of internally proper and stable systems’, 9^th IFAC World Congress, Budapest, Hungary, Vol. 8, pp. 94-98.
• Morari, M. and Zafiriou, E. (1989) Robust Process Control, Prentice-Hall, New Jersey, Englewood Cliffs.
• Packard, A. and Doyle, J. (1993) ‘The complex structured singular value’, Automatica, Vol. 29, pp. 71-109.
• Prokop, R. and Corriou, J. P. (1997) ‘Design and analysis of simple robust controllers’, Int. J. Control, Vol. 66, No. 6, pp 905-921.
• K. V. Price (1999) ‘An Introduction to Differential Evolution’, in: David Corne, Marco Dorigo and Fred Glover (editors), New Ideas in Optimization, McGraw-Hill, London (UK), ISBN 007-709506-5, pp. 79—108.
• Stein, G. and Doyle, J. (1991) ‘Beyond singular values and loopshapes’, AIAA Journal of Guidance and Control, Vol. 14, No. 1, pp. 5-16.
• Vidyasagar, M. (1985) Control systems synthesis: a factorization approach, MIT Press. Cambridge, MA.
• Zelinka, I (2004) Chapter 7, ‘SOMA - Self Organizing Migrating Algorithm’, in: G. Onwubolu — B.V. Babu, New Optimization Techniques in Engineering, Springer-Verlag.