Abstrakt
Příspěvek se zabývá srovnáním rychlosti matematických výpočtů při hledání extrémů vícerozměrných funkcí. Ke srovnání výkonnosti byly použity dva diametrálně odlišné prostředky pro řešení. Na jedné straně se jedná o softwarové řešení pro matematické simulace Wolfram Mathematica 7, na druhé straně o univerzální programovací jazyk C# [1]. Při hledání extrémních hodnot jedno i vícerozměrných funkcí je ale rychlost provádění matematických operací stěžejní. Na ní totiž záleží rychlost nalezeného extrému. Jako srovnávací prvek tedy bude sloužit počet ohodnocení vícerozměrné funkce za 1 sekundu.
Všechny simulace byly prováděny na jednom PC bez změny jeho konfigurace.
Abstract
Paper showing speed differences of mathematical calculation in application designed for finding extreme values of multidimensional functions. For calculation of speed differences were used two absolutely different software solutions for this application. First, there was Wolfram Mathematica version 7, at the opposite side there is universal computing language C# [2]. In multidimensional function extreme finding application is speed of used solutions very important because speed of these algorithms is in close binding with speed of finding extreme value of multidimensional function. In this paper is for showing of differences used parameter which represented number of calculation multidimensional function for 1 second.
All simulations were processing on one PC without any configuration changes.
Introduction
Question about speed of mathematical operation is so important at this time because we need some software solutions for calculating extreme value of multidimensional problems which we might represented by multidimensional functions with one or more extreme values. More and more of actual World problems we will solve by computers. But in many cases we spend more time with mathematical definition of this problem, but this is only first step. Second step is solution of this problem in some application software. And for this process is speed of used system more important. It is not so extraordinary to solving a problem which is represented by function with 10 or 100 dimensions. For humans is too difficult to imagine how to draw more than 4 or 5 dimensions space, but for computers it is not be a problem. Computers just see 100 parameters of one function. It is not necessary to drawing this problem and trying to imagine 100 dimensions space. If we used computers for finding extreme value of this designed function, we have only one question. This question is how much time computer spends with solution of this problem. This is a question of speed. This question has two main parts. First part is speed of used algorithms second part is speed of computer. But second part will be decomposition to two problems. First problem of this decomposition is speed of used computer. In this case is not so important because speed of present computers will be changed very fast. Second part of this decomposition is speed of used application. In many cases is this problem very important because we might saw that software cannot effectively use power of computer. In this case we might use most powerful computer in the World and we do not speed up this calculation.
Question of speed is probably most important question of present computer world in many parts of computer sciences.
Specification of testing environment
For testing was used personal computer with specification shown in Table 1.
|
CPU |
Intel i7 920@2,83GHz (4 cores , 8 threads) |
|
RAM |
6GB DDR II – 1600MHz |
|
HDD |
RAID5 volume (approx. read 170MB/s, write 150MB/s) |
|
Graphic card |
NVidia GeForce 9600GT 1GB VRAM( 64 CUDA[3] 3.0 cores) |
|
Operation System |
Microsoft Windows 7 Professional |
|
|
|
|
Wolfram software |
Mathematica 7 |
|
Program language |
C# .Net Framework 4.0 |
Table 1 - Computer specification
Extreme finding methods were writen in Mathematica 7 environment and C#. Both codes was similar. There was only changes with number of operation for calculating extreme value. Language c# does not has wide mathematic library as Mathematica and some algorithm must be solved with custom functions. Code written in c# is longer than in Mathematica 7.
Used method is not so important because in this paper is used speed of calculation function value for showing doferences between both solution.
Competition situation is shown on Figure 1. This tests were only between Mathematica 7 and C# language.

Specification of testing method
Test procedure was decomposed to 3 parts. In Mathematica 7 environment were tested 10 and 20 dimensions function. In C# language environment were tested 10, 20 and 50 dimensions function because simulation was faster than in Mathematica 7.
In first part were tested speed differences between applications which using only one thread. In this case is evolution of computer power totally blocked because modern computer used more than 1 thread (or core) inside computer processor unit.
In second part used all accessible threads in computer (8 threads on testing computer). In this solution must be possible to parallelize used algorithm. Extreme finding algorithms for multidimensional function is easy parallelized because it is composed from many same operation in which algorithm calculate value on specific coordinates. In this case is possible to maximally use power of computer. In these test we used all processor cores (threads). As parallelization of used algorithms was used automatic parallelization function in both applications. In Mathematica 7 was used function “Parallelize[]”. In C# language was used build in function “Parallel.For()”; There was not any manual changes for main testing algorithm.
Third part shall describe future solution for using graphic card for this calculation. In this part will be described potential of modern graphic cards for specific part of mathematical calculation.
Testing reports
Single thread Mathematica 7
In this part was tested single thread version of testing algorithm. In Mathematica 7 were tested only 10 and 20 dimensions functions.
Results of 10 dimensions simulation are shown in Table 2. During simulation were calculating more than 2,8 million values of testing function, which took more than 13 minutes.
|
Simulation |
10 |
|
Dimensions |
10 |
|
Calculating value |
2 861 760 |
|
Time |
13m 41s (821s) |
|
Calculation/sec |
3 485.7 |
Table 2 - Simulation result 10D Mathematica 7(Single thread)
Results of 20 dimensions simulation are shown in Table 3. In simulation were calculating 8 million values of testing function, which took more than 1 hour.
|
Simulation |
10 |
|
Dimensions |
20 |
|
Number of calculation |
7 963 040 |
|
Time |
1h 10m 36s (4 236s) |
|
Calculation/sec |
1 879.8 |
Table 3 - Simulation result 20D Mathematica 7(Single thread)
On Figure 2 is CPU history usage graph during simulation. This is simulation which running only in one thread. But there is not any full usage CPU core. Single thread if this application does not be so effective. In this case is some unused power of computer.

Figure 2 - Single thread Mathematica 7 during calculation of extreme value
Single thread C#
This is a report of single thread C# language testing. Testing application was created as simple console application for elimination influence of graphic user interface. Application was crested as single thread application without any parallel section. Code of these testing algorithms was larger than in Mathematica because C# language does not contain some mathematical function such as random real generator with specific range and precision.
Testing report from 10 dimensions simulation is shown in Table 4. Simulation used more than 79 million of calculation testing function and took approx. 8 minutes.
|
Simulation |
10 |
|
Dimensions |
10 |
|
Calculating value |
79 055 739 |
|
Time |
7m 42s (462s) |
|
Calculation/sec |
171 116.3 |
Table 4 - Simulation result 10D C# (Single thread)
Test with 20 dimensions produced more than 158 million value of testing function. This simulation set took more than 17 minutes. Result is shown in Table 5.
|
Simulation |
10 |
|
Dimensions |
20 |
|
Calculating value |
158 513 565 |
|
Time |
17m 29s (1049s) |
|
Calculation/sec |
151 109.2 |
Table 5 - Simulation result 20D C# (Single thread)
Last simulation set contain 10 simulation of 50 dimensions function. Test produced approx. 400 million values of testing function and took more than 1 hour. Result is shown in Table 5.
|
Simulation |
10 |
|
Dimensions |
50 |
|
Calculating value |
397 474 241 |
|
Time |
1h 4m 14s (3854s) |
|
Calculation/sec |
103 132.9 |
Table 6 - Simulation result 50D C# (Single thread)
On Figure 3 is CPU history usage graph during simulation. This is simulation which running only in one thread. But there is not any full usage CPU core. Single thread if this application does not be so effective. In this case is some unused power of computer. But operation system use more than one core for calculation. Single thread application in this case can use more computing capacity than used Mathematica. This difference was more than 100%. Single thread application in C# language was better optimized for running on multicore processors.

Figure 3 – Single thread C# during calculation of extreme value
Multi thread Mathematica 7
This part is based on test report with usage of build in automatic parallelization function on both “languages”. First report was from Mathematica with usage of build in function “Parallelize[]”. Test was same. Ten simulations with 10 and 20 dimensions testing function. First test report from 10D function is shown in Table 6.
|
Simulation |
10 |
|
Dimensions |
10 |
|
Calculating value |
3 295 360 |
|
Time |
18m 35s (1115s) |
|
Calculation/sec |
2 955.5 |
Table 7 - Simulation result 10D Mathematica 7(8 thread)
Second test with Mathematica was on 20 dimensions test function. For parallelization was used function “Parallelize[]”. Report from this test is shown in Table 7.
|
Simulation |
10 |
|
Dimensions |
20 |
|
Calculating value |
5 529 280 |
|
Time |
51m 31s (3091s) |
|
Calculation/sec |
1 788.8 |
Table 8 - Simulation result 20D Mathematica 7(8 thread)
Figure 4 shown CPU usage graph during this calculation. Hovever automatic function can not switch usage to all cores of processor. On picture is shown that application used only 3 cores. One for 75 % and others for 20%. Limit of power is approx. Same that in single thread version. No power up. There was a little decreasing of power because part of process was consume for paralelization and synchronization of all threads.

Figure 4 - Multi thread Mathematica 7 during calculation of extreme value
Multi thread C#
These tests were done with multithread version of test algorithm in C# language. From version 4.0 there was function for parallelization of cycles. For test was used function “Parallel.For()”. There were three tests, first with 10 dimensions function, second with 20 dimensions function and third with 50 dimensions function.
Report from first test with 10 dimensions testing function is shown in Table 8. Simulation produced more than 78 million values of function and took approx. 4 minutes which is approx. 50% of time which took single thread version.
|
Simulation |
10 |
|
Dimensions |
10 |
|
Calculating value |
78 572 619 |
|
Time |
3m 58s (238s) |
|
Calculation/sec |
330 137 |
Table 9 – Simulation 10D C# (8 thread)
Test report which used 20 dimensions function is shown in Table 9. This test produced more than 157 million values of testing function and took approx. 9.5 minute which is approx. 55% of time which took single thread version of application.
|
Simulation |
10 |
|
Dimensions |
20 |
|
Calculating value |
157 422 707 |
|
Time |
9m 30s (570s) |
|
Calculation/sec |
276 180.2 |
Table 10 – Simulation 20D C# (8 thread)
Last test used 50 dimension test function. Report was shown in Table 10. This simulation set produced approx. 400 million value of tested function. Simulation set took approx. 34.5 minutes which is less than 50% of time witch took single thread version.
|
Simulation |
10 |
|
Dimensions |
50 |
|
Calculating value |
396 027 020 |
|
Time |
34m 32s (2072s) |
|
Calculation/sec |
191 132.7 |
Table 11 – Simulation 50D C# (8 thread)
Figure 5 showing CPU usage graph during calculation extreme value with multithread version of test algorithm created in C# language. Application can used all computing capacity on each available processor cores in computer. This version of algorithm was core independent and it was easy used on other systems without any rebuilding. Multithread application was more than 2 times faster than single thread. Some of this calculation capapcity was lost with synchronization between thread and for parallel operation function but speed of algoritms increased.

Figure 5 - Multi thread C# during calculation of extreme value
Comparison of speed
This part compares speed differences between both technologies. In first part is comparison between single thread versions of testing application. Differences were shown in Table 11 and on Figure 6.
|
Test |
Mathematica 7 |
C# 4.0 language |
|||
|
Dimension |
10 |
20 |
10 |
20 |
50 |
|
Calculating |
2 861 760 |
7 963 040 |
79 055 739 |
158 513 565 |
397 474 241 |
|
Time |
13m 41s |
1h 10m 36s |
7m 42s |
17m 29s |
1h 4m 14s |
|
Calculation/sec |
3 485,7 |
1 879,8 |
171 116,3 |
151 109,2 |
103 132,9 |
Table 12 - Single thread comparison
This part is more objective that second part, because it is independent on used automatic parallel function. But in table are differences well show. Speed in C# is more than 50 times faster.
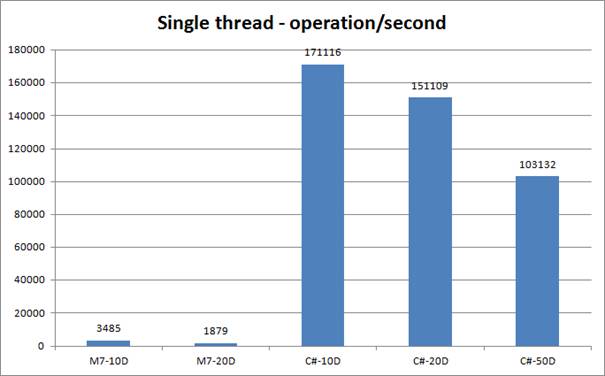
Figure 6 - Single thread - operation/second
Second part contains simulation with multi thread versions of testing methods. In this test is little problem with automatic parallelization function in Mathematica 7 which does not any effect. But increasing of multithread of C# application was very good shown. Summary reports from multithread tests were shown in Table 12 and on Figure 7.
|
Test |
Mathematica 7 |
C# 4.0 language |
|||
|
Dimension |
10 |
20 |
10 |
20 |
50 |
|
Calculating |
3 295 360 |
5 529 280 |
78 572 619 |
157 422 707 |
396 027 020 |
|
Time |
18m 35s |
51m 31s |
3m 58s |
9m 30s |
34m 32s |
|
Calculation/sec |
2 955,5 |
1 788,8 |
330 137 |
276 180,2 |
191 132,7 |
Table 13 - Multi thread comparison
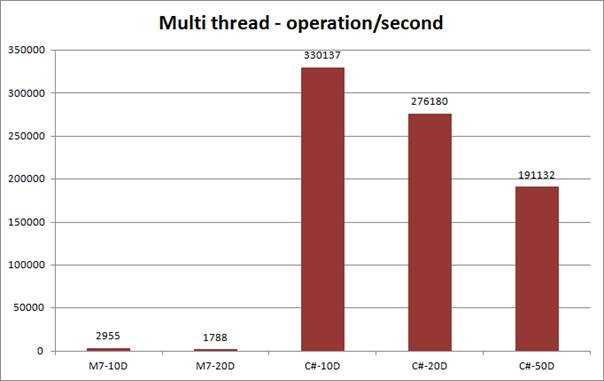
Figure 7 - Multi thread - operation/second
Summary graph with both versions of application is shown on Figure 8.
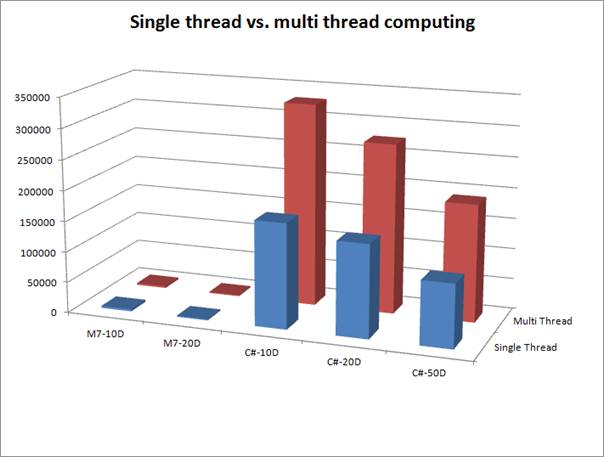
Figure 8 - Single thread vs. multi thread - operation/second
Figure 9 show time of single thread simulation set. Interesting is that c# simulation was more calculation values than Mathmeatica simulation set (more than 25x).
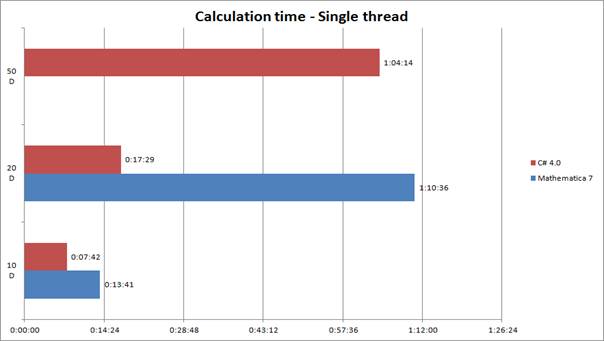
Figure 9 - Single thread - calculation time
Figure 10 show time of multi thread simulation set. Interesting is that c# simulation was more calculation values than Mathmeatica simulation set (more than 25x).
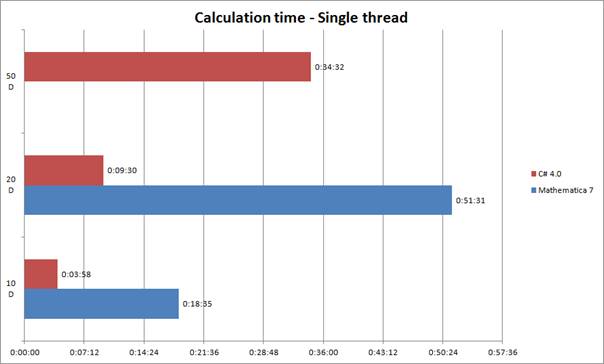
Figure 10 - Single thread - Calculation time
Summary
|
Mathematica 7 |
|
|
Advantages |
Disadvantage |
|
more precission – found extreme value with hight precission |
speed |
|
better visualisation functions |
less CPU usage in single thread application |
|
oriented to mathamatic function |
unstable parallel function |
|
easy for usage |
|
Table 14 - Summary Mathematica 7
|
C# 4.0 framework |
|
|
Advantages |
Disadvantage |
|
speed |
less numerous precission |
|
better usage of CPU in sigle thread applications |
no visualization tools (might use WPF[4], SilverLight) |
|
better parallel optimalization |
less mathematical functions |
|
easy extendable |
coding oriented |
|
free tools for coding |
|
Table 14 - Summary Mathematica 7
Next steps for speedup
Next possible step for speedup of these algorithms for finding extreme value of multidimensional function is porting these algorithms to NVidia CUDA platform which might use graphic cars processor for parallel computing. Modern graphic card contain 480 parallel CUDA computing cores so one card might use 480 thread for computing. This number of available thread might be solutions for “cheap” supercomputing for calculating extreme functions values. If is it possible to parallelize searching algorithm and using multithread version of it, it is possible to transform code to CUDA platform and increase speed of this algorithm. At present time is CUDA platform in very fast evolution steps and it shall be used for parallel computing very soon. In test on testing computer was speed up in computing on graphic card more than 35x. Graphic card inside computer contain only 64 CUDA cores. In specific calculation is this graphic card equivalent to 128 cores CPU system. Graphic card with 480 shall be equivalent to 960 cores CPU system. There is only one specific problem of this platform; this platform is not variable as classic CPU platform. It shall be used only for specific process.
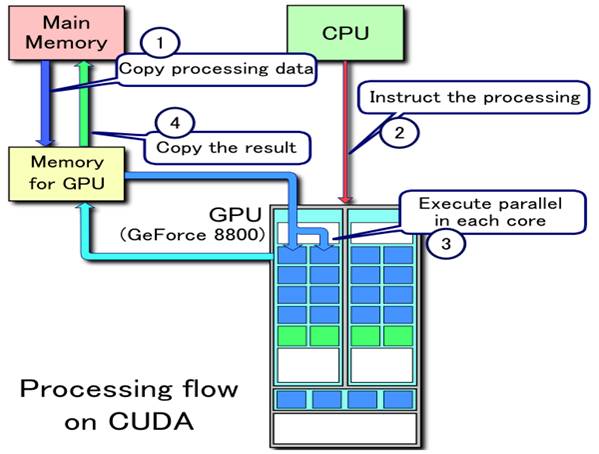
Figure 11 - Processing flow on CUDA
Conclusion
This paper tried describe speed differences between Wolfram Mathematica 7 as a mathematics program environment and universal C# version 4.0 programing language. First environment is developed for mathematic operation and have better library of mathematic function and features for mathematic operation with vectors and graphic object. But result of tests showed that speed of these solutions is completely different. Mathematica had better environment for functions but in speed is slow. In opposite side is C# 4.0 universal program environment. Not so easy for coding but it is very fast. In C# is not a complex library with all mathematics function. Program library is small but it is possible to coding missing procedure and functions.
Result of these tests are: for best precision and visualization is best choose in Wolfram Mathematica, but for very fast calculation of values is the best solution application coding in C#. Solution in C# can better used calculation capacity of testing computer system.
Acknowledgement
Publication of this work was supported by the research grant No. IGA/57/FAI/10/D.
References
[1]Použítá verze 4.0
[2]Used in version 4.0
[3]parallel computing architecture developed by NVIDIA
[4]Windows presentation Foundation
Aktuální číslo
Odborný vědecký časopis Trilobit | © 2009 - 2026 Fakulta aplikované informatiky UTB ve Zlíně | ISSN 1804-1795