Možnosti faktorizace velkých čísel - Shorův algoritmus

Petr Lukašík

Univerzita Tomáše Bati ve Zlíně
Fakulta aplikované informatiky
Nad Stráněmi 4511
760 05 Zlín
Česká republika

plukasik@tajmac-zps.cz

Abstrakt: - Kvantové vlastnosti hmoty otevírají nové možnosti v celé řadě konkrétních aplikací. Jednou z velmi slibně se rozvíjejících oblastí jsou výpočetní jednotky založené právě na kvantových vlastnostech fotonů nebo elektronů. Na základě této skutečnosti se velmi slibně rozvíjejí i algoritmy využívající masivních paralelních vlastností kvantových částic. Částicová fyzika je nejvíce se rozvíjející vědní disciplínou, která zasahuje prakticky do všech oblastí lidských činností a umožnila nebývalý rozvoj všech ostatních oborů.

Abstract: - Quantum properties of matter, opened a new possibilities in many areas. Quantum computing is one of interesting applications, based on quantum properties of photons or electrons. Based on , are developed some interesting algorithms, using massive parallel feature quantum particles. Quantum physics is the most growing sector. Extends to all areas and, allow the development all branches.

Klíčová slova: - Shorův algoritmus, kvantové výpočty, qubit, Zehnderův interferometr, Blochova sféra

Nositel Nobelovy ceny za sjednocení slabé a elektromagnetické interakce Steven Weinberg ve své knize Snění o finální teorii [8] uvedl citát:

“Asi tak před rokem, když jsem čekal na výtah s Philipem Candelsasem (z fyzikálního oddělení Texaské univerzity) stočila se řeč na mladého teoretika , který byl slibným postgraduálním studentem, než zmizel z očí. Ptal jsem se Phila, co překáželo tomuto bývalému studentovi ve výzkumu. Phil smutně potřásl hlavou a řekl: Snažil se pochopit kvantovou mechaniku”.

1. Princip kvantového výpočetního systému.

Kvantový výpočetní systém využívá kvantových vlastností částice, (elektronu, fotonu) jako nositele informace. V klasickém výpočetním systému se využívá deterministického přístupu kódování informace na základě binárního kódu, jehož hodnotami jsou předem dohodnuté dvě hladiny napětí, které představují základní informační jednotku - bit. Kvantově mechanický přístup definuje informační jednotku - qubit, která může nabývat nekonečné množství hodnot mezi nulou a jedničkou. To v praxi představuje, že qubit v uzavřeném kvantovém systému nabývá všech možných hodnot a to v jediném časovém okamžiku. Tento jev je prakticky nepochopitelný a je brán jako fakt. Vypadá to v praxi, že kvantová částice má takové vlastnosti, že se pohybuje z místa A do místa B po všech možných drahách zároveň. Výsledek je následně získán tak, že kvantový systém je podroben měření. To je také velmi zajímavá kapitola chování kvantových částic. Díky měření získáme jediný výsledek žádané výpočetní operace. To znamená, že měřením přejde kvantový systém do stavu, který odpovídá našim zkušenostem. Podivné chování uzavřeného kvantového systému lze demonstrovat na Mach Zehnderově interferometru. [3][7][4] 1)* Získání výsledku je však v důsledku existence principu neurčitosti kvantového systému velmi obtížné.

1)*

Výše uvedené vlastnosti byly mnohokrát experimentálně potvrzeny. Tyto experimenty jsou však velmi obtížné. To souvisí především s problémem přípravy jednofotonových stavů světla [1]

Tento přístup připomíná princip analogového počítače, který byl využíván pro modelování dynamických jevů v oblasti regulace. Klasický analogový počítač však postrádá masivní paralelismus, který je ovšem kvantovému počítači vlastní. Obecně, každá klasická výpočetní operace (NAND, XOR) je prováděna nevratným způsobem. To znamená, že se nelze vrátit na začátek výpočtu, nebo dokonce nelze rekonstruovat z jakých vstupních hodnot vznikl výsledek. Obecně víme, že výsledkem operace NAND jsou dvě vstupní hodnoty, přičemž pro logickou jedničku nezáleží zda byla logická nula na jednom ze vstupů a na kterém, nebo na obou důležitý je výsledek. To vede jednoznačně ke ztrátě informace a nárůstu entropie systému, který se díky tomuto jevu zahřívá. Tím je určena technologická hranice klasických výpočetních systémů, která je právě omezena nárůstem vnitřního odporu křemíkových čipů při snižující se velikosti jednotlivých konstrukčních prvků.

Každá operace s qubity odpovídá vývoji v čase nějakého uzavřeného kvantového systému. Tyto operace splňují podmínku transformací, které jsou popsány unitárními operátory, pro které platí:

kde I je jednotkový operátor. Z toho vyplývá, že každou kvantovou výpočetní operaci lze nechat běžet i reverzibilně. To znamená, že je možno rekonstruovat stav před výpočtem. To je velký rozdíl proti klasickým počítačům. V důsledku toho, nedochází ke ztrátě informace. Tím ovšem vzniká jiný problém, protože díky této vlastnosti nelze v kvantovém počítači vynulovat registr (což je v klasickém počítači triviální operace). Operace nulování není unitární. V praxi to znamená, že nemůžeme libovolně nulovat kvantový registr pro další použití. V kvantovém počítači lze nulovat jen inverzní operací k tzv. operaci FANOUT (rozfouknutí) a to tak, že ze dvou kopií vytvořit jedinou s tím, že jeden bit se vynuluje. To znamená, že je nutné mít dostatečné množství registrů pro ukládání nepotřebných informací. [5][2]

Jakkoliv nalezené kvantové algoritmy vypadají slibně, jejich zásadní problém spočívá v tom, že není vůbec snadné takový kvantový systém sestrojit. Kvantové bity jsou buď velmi citlivé na rušivé vlivy okolí, nebo je značně obtížné je přinutit, aby spolu navzájem komunikovaly. Má-li být kvantovou informací například spin elektronu, musíme jej velmi dobře izolovat od okolí. To znamená, že musíme zajistit uzavřenost systému, který umožňuje provádět unitární operace a tedy kvantové výpočty. Dalším problémem jsou fázové posuvy při interakci atomů s okolím. Kvantové superpozice jsou velmi křehké. V tom také spočívá jedna z odpovědí, proč nepozorujeme Schrödingerovy kočky, tedy superpozice dvou různých stavů (živá a zároveň mrtvá) u makroskopických objektů. Vlivem i nepatrné interakce s okolím, se systém dostává do jednoho z normálních stavů, které jsme zvyklí pozorovat.[5]

2. BIT - PBIT – QUBIT.

Klasický bit jako jednotka informace definuje pouze dva stavy 0 a 1. Pbit jako pravděpodobnostní bit tvoří základní jednotku Fuzzy logiky a nabývá pravděpodobnostní hodnoty ve škále od 0 do 1.

Qubit se liší tím, že zahrnuje také všechny kvantové superpozice těchto dvou základních stavů. Umožňuje informaci, kódované nulou a jedničkou ležet v tzv. Kombinovaných stavech, které se v souladu s konvencemi kvantové fyziky popisují tzv. Diracovou symbolikou |0> a |1>. Díky tzv. kvantové superpozici (viz Mach Zehnderův interferometr) nabývá hodnot |0> a |1> zároveň. Tyto kombinace kvantových stavů qbitu jsou popsány vlnovou funkcí:

(1)

Kde α a β jsou komplexní čísla, pro něž platí . Čísla α a β představují amplitudy pravděpodobností výskytu kvantové částice.

Zjednodušeně je možné stavy qubitu přirovnat k hodu mincí, při níž platí jakákoliv kombinace možných výsledků. To znamená panna, orel, panna nebo orel nebo jakákoliv možná kombinace mezi pannou a orlem. Tento zvláštní stav je kvantovým částicím vlastní.[5]

Stav qubitu je možno zjistit měřením. To však vždy dá buď hodnotu |0> nebo hodnotu |1>. Žádným měřením nelze zjistit hodnoty amplitud pravděpodobností. Problémem je, že jakékoliv měření naruší kvantový stav qubitu. Dochází k tzv. kolapsu vlnové funkce. V důsledku tohoto procesu se informace o původním stavu nezachovává. Obecně si lze velmi těžko představit co tento specifický problém v oblasti kvantové mechaniky představuje. Platí však následující. Existuje - li kvantový systém, který se nachází v několika pro nás nerozlišitelných stavech, nachází se tento systém v kvantové superpozici všech těchto stavů. Tuto superpozici lze popsat vlnovou funkcí systému. Získáme-li však nějakým způsobem informaci o stavu systému, například měřením, dojde k porušení vlnové funkce. To má přímou souvislost s tzv. kvantovou dekoherencí, která vyplývá z Heisenbergova principu neurčitosti. Velmi dobře je tento problém popsán s pomocí dvojštěrbinového experimentu, který je modifikován zdrojem záření mezi dvojštěrbinovým stínítkem a detektorem záření. [3]. Právě Peter Shor z AT&T a Andrew Steane z Oxfordské univerzity, ukázali, jak lze kvantové stavy narušené měřením opravit tzv. kvantovou provázaností (entanglement). Entaglement představuje další fenomenální vlastnost hmoty, kdy jednotlivé subsystémy (například elektrony) jsou vzájemně korelovány. Pokud na konkrétní částici provedeme měření a změníme její vlastnosti (například spin) změna se okamžitě projeví i na druhé částici, která je s touto částicí korelována. Rychlost změny je však ovlivněna rychlostí světla. Pro qubit to znamená, (jak bylo poznamenáno výše) že pokud se nacházi ve stavu superpozice, pak není ani ve stavu |0> ani ve stavu |1>, dokonce ani mezi stavy |0> a |1>. Ve skutečnosti se nachází ve stavu |0> i |1> zároveň. A na tomto principu je založen kvantový počítač, který díky této zajímavé vlastnosti uzavřeného kvantového systému (qubitu), je schopen provést jednu operaci s velkým počtem hodnot. To v praxi znamená že je schopen provádět obrovské množství paralelních výpočtů. Výsledek se dozvíme tím, že stav uzavřeného kvantového systému změříme. Tím kvantový systém tzv. otevřeme, což ovšem představuje zásadní problém, který dělá z kvantového počítačového systému velmi obtížně fyzikálně realizovatelný systém. Znamená to totiž, že měřením ztratí kvantový systém své kvantové vlastnosti a tedy i informaci o výsledku výpočtu. Mluví se o tzv. kvantové dekoherenci. Tento jev popsán v [3]. Nicméně, pokud se měření (tedy výpočet) provede dostatečně rychle, je možné získat výsledek (s určitou pravděpodobností) ještě dříve, než kvantový systém upadne do dekoherence.

Kvantové počítače patrně nebudou univerzálními stroji, ale budou konstruovány jako konečné automaty pro konkrétní typy úloh a budou muset zajistit velké množství samoopravných mechanismů k získání relevantního výsledku. Zatím nejvýkonnější kvantový počítač D-Wave má 128 Qubitový procesor, který využívá principu Josephsonových smyček. Ty pracují na principu tunelování elektronových párů mezi dvěma supravodiči z niobu. Nelze předpokládat, že končí doba tranzistorů. Ty budou zcela určitě ještě dlouhou dobu základním konstrukčním prvkem. Ale principy, které ukazuje kvantová fyzika jsou velmi zajímavé.

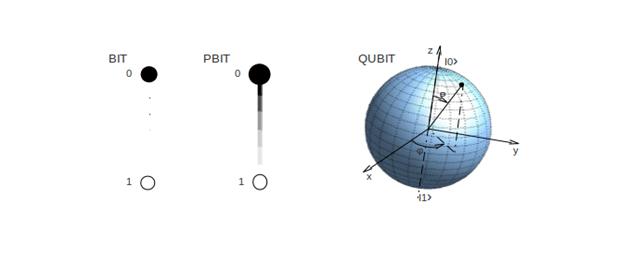
Obrázek 1: Znázornění qubitu - jednotky informace v kvantové podobě

3. Blochova sféra.

Blochova sféra je geometrická interpretace stavů qubitu. Principiálně vychází z podobné tzv. Poincarého sféry, jejíž princip je využíván v oblasti polarizace elektomagnetických vln.[1] Je oblíbenou pomůckou pro znázornění jednoho qubitu na povrchu sféry. Každý bod na povrchu sféry představuje jeden stav qbitu, přičemž severní a jižní pól představuje stavy |0> a |1> , tedy stavy, kterých nabývá klasický bit. Obecný stav vlnové funkce |Ψ> lze získat zadáním úhlů φ a 2Θ. Libovolný qubit lze matematicky popsat následující formulí.

(2)

jsou reálná čísla. Číslo definuje bod na povrchu Blochovy sféry. Číslo lze volit tak aby (platí pro pak se definice qubitu následně zjednoduší.[5]

(3)

4. Shorův algoritmus

První kvantový algoritmus, který vyvolal velkou vlnu zájmu o kvantové výpočty. Byl zveřejněn Peterem Shorem (MIT) v roce 1994. Byl zajímavý tím, že ukázal praktické využití kvantových výpočtů. Jádrem Shorova algoritmu je diskrétní Fourierova transformace, která umí zjistit, zda nějaká diskrétní funkce je periodická a jakou má periodu. Pro nalezení periody diskrétní funkce se právě využívá masivních paralelních výpočtových vlastností kvantového systému. Tím byla nastíněna cesta, jak pokořit princip asymetrického šifrovacího systému, který je založen na principu geometrického nárůstu času potřebného k rozluštění šifry v závislosti na délce klíče. Tedy roste - li délka klíče lineárně, čas potřebný k rozbití šifry hrubou silou (to znamená testováním všech možností) narůstá geometricky. K takto obtížným algoritmům se řadí právě RSA, který využívá triviální výpočetní operace násobení dvou čísel a velmi obtížné inverzní operace - faktorizace, která umožní získat původní činitele, z něhož výsledek vznikl. Obecně sice nebyl podán důkaz, že existuje nekvantový algoritmus, který tuto úlohu řeší, což znamená, že takový algoritmus může existovat, ale zatím stále odolává nalezení.[6]

Ovšem Shorův algoritmus ukazuje cestu, jak faktorizaci provést v tzv. polynomiálním čase a to za pomocí výše zmíněného kvantového výpočetního systému. Cílem tohoto článku není detailní popis kvantového principu algoritmu, ale popis jednotlivých sekvencí s možností simulace na klasickém výpočetním systému.

Faktorizaci malých čísel lze efektivně provádět Euklidovým algoritmem Význam Shorova algoritmu nastupuje v okamžiku velkých čísel, kde již klasický Euklidův algoritmus naprosto selhává. Nutno upozornit, že má statistický charakter, což znamená, že neexistuje přesná kuchařka při zadání vstupních hodnot pro faktorizaci. To znamená, že řada kombinací čísel potřebných k výpočtu nemusí vždy vést ke správnému výsledku. Ale metoda pokusů a omylů (nalezení periody posloupnosti) dává velkou pravděpodobnost získání relevantního výsledku.

1.4.1 Shorův algoritmus - nalezení periody diskrétní funkce

Principem Shorova algoritmu je nalezení periody posloupnosti, která je výstupem počítání operace modulo nad čísly N a r, kde r je libovolné zvolené číslo nesoudělné s N, přičemž číslo N je to, které chceme faktorizovat. Pro čísla soudělná tento algoritmus nefunguje, protože nalezení tohoto čísla je řešením problému. RSA využívá vlastností násobení dvou velkých prvočísel (přesněji dvou prvočísel s velkou pravděpodobností), kdy je zaručeno, že faktorizací tohoto násobku jsou právě a pouze tato prvočísla. V tomto případě existuje téměř nulová pravděpodobnost nalezení takového prvočísla přímo. Pak tedy nastupuje Shorův algoritmus, který dává řešení.

Posloupnost

(4)

je vypočítávána dle vzoru:

(5)

A je zajímavá tím, že je periodická. To plyne z faktu, že tuto posloupnost lze přepsat do tvaru

(6)

To se dá ověřit na faktorizaci čísla N=15 a zvoleného čísla r=7.

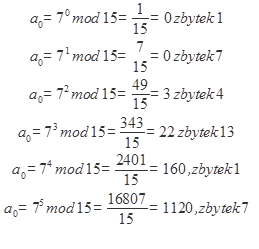
Z této posloupnosti na první pohled vyplývá sudá perioda o velikosti 4. Pokud však budeme chtít faktorizovat opravdu velké číslo, musíme výslednou posloupnost podrobit výpočtu kvantové Fourierovy transformace, která periodu nalezne. Ta poslouží jako vstup k výpočtu největšího společného dělitele čísla N. Číslo r, které do algoritmu také vstupuje, musí být zvoleno tak, aby byly splněny následující předpoklady.

1. Číslo z musí být nesoudělné s číslem N

2. Výsledek spočítané periody musí být sudé číslo

3. V periodě se nesmějí vyskytovat čísla které jsou v rozsahu N+1 a N-1.

Toho lze právě docílit pouze metodou pokusů a omylů, kdy některá zvolená čísla nevedou k výsledku, takže musí být voleno číslo jiné.

5: Závěr

V blízké budoucnosti zatím nehrozí konstrukce univerzálního kvantového počítače, který by plně nahradil současný svět výpočetní techniky. Bude se spíš jednat o konstrukce speciálních konečných automatů zaměřených na řešení konkrétní úlohy. Je však patrné, že být vizionářem v této oblasti je nesmírně těžké, nebo se přinejmenším nevyplácí. Takže kdo ví, co přinese brzká budoucnost.

Reference:

[1] Aspect, A.; Grangier, P.: Wave-particle duality for single photons. Hyperfine Interactions, Vol. 37, s. 3„ 1987.

[2] Bennett, C.H.; DiVincenzo, D.P.: Quantum information and computation. NATURE VOL 404 16 MARCH 2000, ročník IBM Research Division, T. J. Watson Research Center, Yorktown Heights, New York 10598, USA: s. 247–255. URL www.nature.com

[3] FEYNMAN LEIGHTON SANDS: Feynmanovy přednášky z fyziky. California Institute of Technology, USA, 1964.

[4] HEY, T.; WALTERS, P.: Nový kvantový vesmír. Cambridge University Press, Cambridge 2003, 2003.

[5] NIELSEN, M.A.; CHUANG, I.L.: Quantum Computing. Cambridge University Press, Cambridge 2000, 2000.

[6] OPATRNÝ T.; RICHTEREK L.: Vybrané partie současné fyziky. Katedra teoretické fyziky Přírodovědecká fakulta Univerzita Palackého, 2005.

[7] PavelCejnar : Kvantové hlavolamy. Vesmír 77, ročník 3, 1998: str. 129. URL http://www.vesmir.cz/clanek/kvantove-hlavolamy-i

[8] Weinberg Steven : Snění o finální teorii teorii. Hynek, 1999.

[1] Poincarého sféra je grafický nástroj, který umožňuje znázornit polarizaci signálů a polarizačních transformací. Dobrá pomůcka například při návrhu polarizace anténních zářičů