Homografie a epipolární geometrie

Klasický problém počítačového vidění je rekonstrukce 3D scény ze dvou či více snímků. Elementární úlohou je proto stereo korelace,  neboli potřeba definování množství dvojic odpovídajících si bodů ze stereo páru. V tomto článku je popsána metoda významně usnadňující hledání takovýchto bodů. Zmíněná metoda, epipolární geometrie, vychází z projektivní lineární transformace. Pro snazší pochopení souvislostí jsou tedy uvedeny postupně obě problematiky ve vzájemné návaznosti.

 

Abstract

The classic problem of computer vision is the reconstruction of 3D scene from two or more images. The elemental task is a stereo correlation which means determination of the set of point correspondences in the two views. This article describes the method greatly facilitates the search for such points. The above method, epipolar geometry, is based on a projective linear transformation. For an easier understanding of the connections are thus gradually given both theories in mutual relationship.

1 úvod

Stále zrychlující tempo rozvoje robotiky v posledních letech s sebou přináší potřebu vylepšení stávající úrovně v oblasti senzoriky. Velmi perspektivní částí této oblasti je počítačové vidění, jež se zabývá extrahováním potřebných informací z digitální obrazové informace. Takové informace tvoří zpravidla údaje o předmětech na snímané scéně, jejich tvaru, účelu a vzájemné vzdálenosti. Zpracováním těchto dat je možné rekonstruovat okolí a umožnit tak například efektivní řízení pohybu mobilního robotu, nebo sledování předem definovaného pohyblivého předmětu, cíle. Stereovizní kamerový systém se ukazuje býti v této oblasti velmi efektivním, neboť díky dvojici snímků lze pasivním způsobem dopočítat pozici snímaných objektů v prostoru nezávisle na vzájemném relativním pohybu kamerového systému a scény. Aby bylo možné prostorové vzdálenosti dopočítat, je nutné najít ve stereo páru dostatečné množství stereo korespondencí, tedy 2D bodů v levém a pravém obraze, které jsou projekcemi stejného 3D bodu na scéně. Existuje množství metod nalezení korespondencí lišící se chybovostí i vhodností použití v nejrůznějších situacích. Tento článek se snaží čtenáři přiblížit základní geometrii dvou pohledů (stereoskopie), ukazuje, jakým způsobem se promítá scéna do jednotlivých průměten kamer a jak je možné výrazně zjednodušit hledání stereo korespondencí.

 

2 projektivní lineární transformace

Projektivní transformace je invertibilní transformace mezi dvěma projektivními perspektivami, kde zásadní vlastností je mapování přímek opět na přímky. Odtud vznikl synonymní název kolinearita, jenž však může mít obecnější význam. Dalšími názvy pro projektivní transformaci, se kterými je možné se v odborné literatuře setkat, jsou projektivita a homografie^[5]. Projektivita tedy vyjadřuje, jak se mění vjem pozorovaného předmětu, pokud se mění pozice a/nebo úhel pohledu pozorovatele^[4].

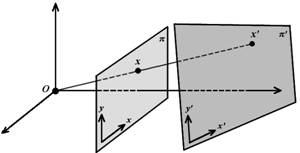
Obrázek 1 Homografie

Příkladem projektivní transformace (viz Obrázek 1) je středové promítání se středem a dvojicí ploch a , jež mapuje body z jedné plochy na body druhé plochy . Z tohoto je zřejmé, že také přímky jedné plochy jsou mapovány opět na přímky druhé plochy. Pro body v homogenních souřadnicích[1] lze toto mapování zapsat jako , kde je transformační matice homografie o rozměru 3x3:

		( 1 )
		( 2 )

           

Obrázek 2 Příklad projektivní transformace – sloučením dvou homografií je opět homografie

2.1 Výpočet homografie

Záměrem je nalézt transformační matici, pro niž platí . Avšak za povšimnutí stojí, že a si číselně neodpovídají, neboť se liší v měřítku (daném homogenní souřadnicí ). Přesto je možné zapsat: . Nahrazením šikmo symetrickým zápisem a separací neznámých dostaneme soustavu:

( 3 )

Tyto rovnice mají podobu kde je matice a vektor . má hodnost 2 (s opominutím měřítka je třetí řádek získán sečtením násobku prvního řádku a násobku druhého), tudíž je každá korespondence vyjádřena dvojicí rovnic.

Složením rovnic pro čtyři body vzniká matice jejíž hodnost je 8 a tvoří lineární homogenní soustavu rovnic pro 9 neznámých. Z toho plyne, že stačí, když matice obsahuje 8 lineárně nezávislých řádků. Řešením je potom nulový prostor této matice. Body musí být zvoleny tak, aby žádné tři neležely na stejné přímce.

( 4 )

V praxi se používá korespondencí více než 4, aby se zmenšil vliv chyby při určení korespondujících bodů. Kvůli chybám je však také nulový prostor matice prázdný a vektor se hledá ve smyslu nejmenších čtverců, tj. určí se jako:

( 5 )

kde je Euklidovská norma . Nalezení vektoru se v takovém případě udělá pomocí SVD (Singular Value Decomposition).^[6]

 

3 Epipolární geometrie

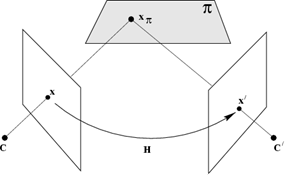
Rekonstrukce 3D scény ze dvou a více rovinných průmětů je klasická úloha počítačového vidění. Elementárním problémem je určení pozice bodu v prostoru pomocí dvojice kamer. Průmětem 3D scény do obrazových rovin těchto kamer vzniká dvojice obrazů nazývaných stereo pár[2]. Teoretickým základem pro určení vzájemného vztahu stereo páru je epipolární geometrie, která je nezávislá na struktuře scény a závisí pouze na vnitřních parametrech kamer a jejich relativní pozici.^[2] Pomocí epipolární geometrie lze bod z prvního obrazu mapovat na přímku v druhém obrazu[3], což značně zjednodušuje nalezení korespondujících bodů (bod z prvního snímku není nutné hledat na celé ploše druhého snímku, ale jen na přímce nacházející se na této ploše).

V zásadě existují dva přístupy k rekonstrukci prostorové scény, tedy k získání fundamentální matice . První možností je určení projekčních matic kamer.  Tento přístup ovšem vyžaduje znalost vnitřních parametrů kamer, jež lze nabýt kalibračními technikami. Druhým přístupem k rekonstrukci 3D scény je využití projektivity (homografie) snímků. Detekcí vzájemně si odpovídajících bodů určíme projektivitu snímků, aniž bychom znali vnitřní parametry kamery.

V obou případech je důležité zvolit model kamery, který co nejpřesněji vystihuje kameru reálnou.

3.1pProjektivní model kamery

Nejjednodušším projektivním modelem kamery, který poměrně dobře aproximuje v současnosti hojně používané digitální mikro-kamery, je „camera obscura“ (z lat. temná komora), tedy dírková komora (nebo v anglické literatuře pinhole camera). Účelem zavedení modelu kamery je potřeba určení způsobu mapování 3D bodu pozorované scény do 2D obrazového bodu kamery.

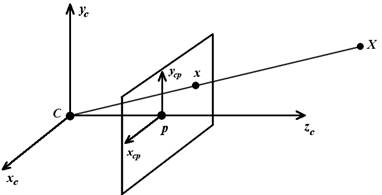
Obrázek 3 Projektivní model kamery

Z Obrázek 3 je patrné, že bod středového promítání je umístěn v počátku souřadného systému kamery. Ve vzdálenosti (ohnisková vzdálenost) od počátku se nachází rovina promítání (průmětna) kolmá na osu , reprezentující optickou osu kamery. Průsečíkem této osy a průmětny je definován principiální bod , jež je zároveň počátkem 2D souřadného systému kamery. Principiální bod se vlivem výrobních nepřesností nemusí shodovat se středem průmětny, v takovém případě se provádí translace souřadného systému do principiálního bodu vektorem . Takto navrženému geometrickému modelu odpovídá mapovaní bodu na . Nebude-li uvažována třetí souřadnice obrazového bodu, jelikož je neměnná, pak:

( 6 )

bude požadované 3D na 2D mapování. V homogenních souřadnicích je možné totéž vyjádřit maticovým zápisem:

		( 7 )

Tato rovnice předpokládá zadání obrazového bodu v souřadném systému kamery, případně souřadném systému průmětny . V praxi může být v některých případech výhodnější uvažovat pozici bodu v obraze na základě pixelových souřadnic a vzniká tak potřeba transformace na takzvaný obrazový (též pixelový) souřadný systém.^[3] Rovnice transformace je:

		( 8 )
		( 9 )

kde a (viz Obrázek 4) udávají počet pixelů na jednotku vzdálenosti. Přidaný parametr vyvažuje zkosení průmětny, pro většinu normálních kamer bude ovšem nulový. Transformační matice se nazývá kalibrační matice ( matice vnitřních parametrů kamery) o pěti stupních volnosti.

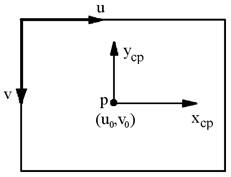
Obrázek 4 Souřadný systém průmětny a pixelový souřadný systém

Model projektivní kamery se skládá nejen z vnitřních parametrů, nýbrž i z vnějších, definujících jak pozici, tak i orientaci kamery vzhledem ke globálnímu systému souřadnic, viz Obrázek 5. Snímaný bod má souřadnice v souřadném systému kamery a v globálním souřadném systému. Přechod mezi systémy může být vyjádřen rotací a translací takto:

( 10 )

Zavedením vektoru , jež určuje pozici středu kamery v globálním souřadném systému lze nahradit vektor . Sloučením transformací (9) a (10) vzniká projekční matice kamery :

		( 11 )
		( 12 )
		( 13 )

Z (13) vyplývá, že bod je tedy udáván v jednotkách vztahujících se ke globálnímu systému souřadnic, zatímco jeho projekcí na průmětnu vytvořený bod je v pixelových souřadnicích obrazového souřadného systému. Projekční matice kamery o velikosti má celkem 11 stupňů volnosti (5 za , 3 za a 3 za ).

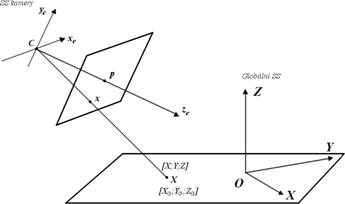
Obrázek 5 Transformace souřadných systémů

3.2 Východiska epipolární geometrie

V prostoru se nachází bod , jenž je snímán dvojicí kamer, jejichž matice jsou a . Bod se promítá na průmětny kamer jako bod a bod tak, že platí a . Spojnice mezi středy kamer a se nazývá báze. Průsečík báze s rovinou průmětny tvoří epipól a (epipól nemusí nutně ležet v zobrazovací výseči kamery). Přímka procházející body a , popř. a je označována jako epipolární přímka a značí se , popř. . Středy kamer, epipóly a body , , jsou koplanární, to znamená, že leží v jedné epipolární rovině viz Obrázek 6.

 

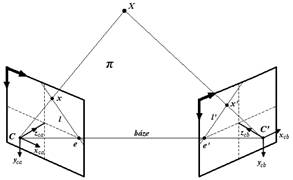
Obrázek 6 Epipolární geometrie

Jak bylo uvedeno, nejdůležitějším důsledkem epipolární geometrie je mapování . Toto je určeno vnitřními geometrickými vlastnostmi, jež jsou interpretovány tak zvanou fundamentální maticí F. Pro každé dva korespondující body platí:

( 14 )

A klíčový vztah pro výpočet epipolární přímky:

( 15 )

Problematice odvození těchto vztahů a výpočtu fundamentální matice je věnována následující podkapitola.

3.3pVýpočet fundamentální matice

Postup mapování může být rozdělen do dvou kroků. V prvním je bod mapován prostřednictvím homografie (Obrázek 1) na nějaký bod ležící na epipolární přímce v jiném obraze. Ve druhém kroku je získána epipolární přímka jako přímka procházející bodem a epipólem . Je-li dán bod , pro epipolární přímku procházející bodem a epipólem lze napsat .[4] Protože může být zapsáno jako :

( 16 )

odtud definujeme fundamentální matici:

( 17 )

kde je homografie v libovolné rovině . Kromě toho protože má hodnost 2 a hodnost 3, bude mít hodnost 2. Fundamentální matice je čtvercová matice , má 7 stupňů volnosti, a tvar 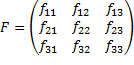. Pro každé dva korespondující body a píšeme rovnici:

( 18 )

Sloučením jednotlivých položek matice do vektoru dostaneme:

( 19 )

Pro -početnou skupinu korespondujících dvojic získáme soustavu lineárních rovnic, jež mají podobu :

( 20 )

Složením rovnic pro osm bodů vzniká matice jejíž hodnost je 8 a tvoří lineární homogenní soustavu rovnic pro 9 neznámých. Z toho plyne, že stačí, když matice obsahuje 8 lineárně nezávislých řádků. Řešením je potom nulový prostor této matice. V praxi se používá korespondencí více než 8, aby se zmenšil vliv chyby při určení korespondujících bodů. Kvůli chybám je však také nulový prostor matice prázdný a vektor se hledá ve smyslu nejmenších čtverců, tj. určí se jako singulární vektor odpovídající nejmenší singulární hodnotě , tj. poslednímu sloupci z získaného SVD metodou ^[5].

4 Závěr

V článku jsou rozebrány teoretické základy stereoskopie, především projektivní transformace jako východiska pro výpočet fundamentální matice vystihující vnitřní geometrii dvou pohledů – epipolární geometrii. Ze znalosti této matice jsme nadále schopni určit mapování bodů z jednoho obrazu na tak zvané epipolární přímky v obraze druhém. Důvodem konstrukce těchto přímek je usnadnění hledání korespondujících bodů; nemusí se nadále hledat v celé ploše obrazu, nýbrž je hledání omezeno na epipolární přímku. Ve spojení s dalšími metodami hledání stereo korespondencí (např. využití detekce hran) je celý proces výrazně zjednodušen a tedy i urychlen, což vede k snížení výpočetních nároků a navýšení počtu stereo snímků zpracovaných v reálném čase.  

PODĚKOVÁNÍ

Tento článek vznikl za podpory grantu IGA Univerzity Tomáše Bati ve Zlíně, Fakulty aplikované informatiky, číslo IGA/47/FAI/10/D, Interaktivní mobilní robotický systém pro bezpečnostní a asistenční technologie.

Reference

1. VORÁČOVÁ, Šárka. Aplikace epipolární geometrie [online]. Praha : ČVUT v Praze, Barborka, 2004. 5 s. Sborník 24. konference o geometrii a počítačové grafice. České vysoké učení technické v Praze, Fakulta dopravní. Dostupné z WWW: <http://www.fd.cvut.cz/personal/voracsar/epipolar.pdf>.

2. ŘÍHA, Kamil; HUJKA, Petr. Epipolární geometrie. Elektrorevue [online]. 21. března 2005, 2005/17, [cit. 2010-08-06]. Dostupný z WWW: <http://www.elektrorevue.cz/clanky/05017/index.html>.

3. BYSTŘICKÝ, Václav. Určení pozice bodu prostoru pomocí dvou kamer [online]. Plzeň : ZČU v Plzni, 2007. 18 s. Oborový projekt. Západočeská univerzita v Plzni, Fakulta aplikovaných věd. Dostupné z WWW: <http://home.zcu.cz/~vbystric/public/Report_2007_APG_Bystricky_Vaclav.pdf>.

4. Homography. In Wikipedia : the free encyclopedia [online]. St. Petersburg (Florida) : Wikipedia Foundation, 1 November 2005, last modified on 26 August 2010 [cit. 2010-09-02]. Dostupné z WWW: <http://en.wikipedia.org/wiki/Homography>.

5. HARTLEY, Richard; ZISSERMAN, Andrew. Multiple View Geometry in Computer Vision. Second. UK : Cambridge University Press, 2004. 655 s. ISBN 0-521-54051-8.

6. DRBOHLAV, Ondřej. Katedra počítačů ČVUT FEL [online]. 2002-12-06 [cit. 2010-09-05]. Výpočet projektivní transformace. Dostupné z WWW: <http://cmp.felk.cvut.cz/cmp/courses/383ZS/ZSO2003-4/cvic3/node4.html>.

7. CRIMINISI, Antonio; ZISSERMAN, Andrew; REID, Ian. Department of Engineering Science, University of Oxford [online]. 1997-07-13 [cit. 2010-09-05]. Computing the plane to plane homography. Dostupné z WWW: <http://www.robots.ox.ac.uk/~vgg/presentations/bmvc97/criminispaper/node3.html>.