Equality Constraints in Predictive Control of Laboratory Model

Tomáš Barot, Marek Kubalčík
barot@fai.utb.cz, kubalcik@fai.utb.cz

Tomas Bata University in Zlín
Faculty of Applied Informatics
nám. T. G. Masaryka 5555, 760 01 Zlín
Czech Republic

Abstract

Predictive control is a modern approach in the system-control theory. It is suitable for many types of controlled systems. Ability for the including of constraints is an important advantage of it. This principle is projected to an optimization problem. Inequality restrictions are commonly used in control applications. In this paper, the less used equality constraints are presented and demonstrated together with their real testing; however, this principle has been researched in some specific studies yet.

Keywords

Predictive Control, Optimization, Inequality Constraints, Equality Constraints.

Introduction

A principle of predictive control [1] is based on the receding horizon strategy [2]. The previous and future information about control are needed for the computation of a control law using a model of a controlled system in each sampling period. Future values are given by prediction equations [3]; however, the requirements for a control [4] must be defined in addition. This phenomenon is solved by an optimization task, where a manipulated variable is determined.

The optimization problem is able to incorporate constraints of signals. If a cost function has a quadratic form and the constraints are defined for its argument, then a quadratic programming problem [5]-[7] is solved. This mathematical task corresponds to the predictive control. However; the possibilities of the quadratic programming are wide, the inequality conditions on variables are more generally used than equation equalities.

Equality constraints [6] are not so widely discussed in the few past years; although, this problem has been researched yet - e.g. in [8]-[9]. A case of inequality restrictions [6] is the most commonly described, e.g. in [3]. In this paper, the implementation of the equality constraints is explained together with its testing in the real conditions.

Model of Controlled System in State-Space

A single-input single-output system is described in a state-space representation (Fig. 1) by matrices A, B, C, D in (1), where n is a number of the state variables in a vector x; y is an output signal, u represents a manipulated-input variable.

(1)

The step response of this model (1) can be evaluated by state-equation (2).

(2)

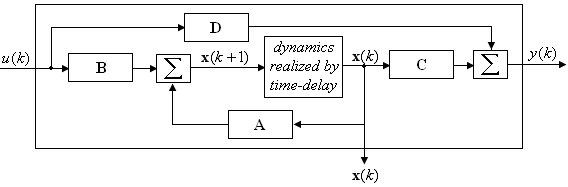
Fig. 1 Scheme of State-Space Description of System

Receding Horizon Strategy in Predictive Control

A predictive-control principle is represented by a specific predictive enumeration on the time interval in the future, as can be seen in Fig. 2. Its length is a maximum horizon N2. In addition, there are a minimum horizon N1 and a control horizon Nu.

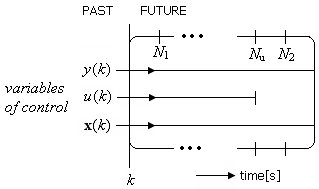
Fig. 2 Predictive Control Strategy Using Horizon Parameters

A control law is based on determination of a minimizing argument in an optimization problem with a quadratic cost function. The result of the optimization is a value of an increment of variable (3). This optimization task is a quadratic programming (4). It is allowed to incorporate the constraints (5) on variables, which are in predictive control.

(3)

(4)(5)

Matrices H and b are determined in (6), (7) and they are based on the optimization and predictive variables in the receding horizon principle.

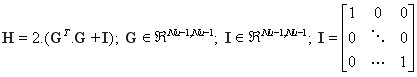(6)

  (7)

Variable is defined for the purposes of an integrating recommendation for the control. Reference signal is defined by w. Matrices P and G are defined as (8) and (9).

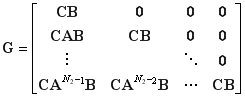(8)(9)

The dynamics of a controlled system is expressed by matrix G. The content of matrices P and G corresponds with a matrix equation (10), which is an equation for the evaluation of the future values of y on the receding horizon.

(10)

Inequality Constraints for Predictive Control

The most commonly used constraints have in predictive control a form of inequalities. The restrictions are defined using (5) for the signal ranges in control. Minimum and maximum values can be defined for variables y, and u. The constraints have a form defined in Table 1. The expressions use the vector of increments of the manipulated variable. Matrices E have all elements equal to one. T is a lower-triangular matrix, where the entries bellow the main diagonal are ones.

Table 1. Inequality Constraints for Quadratic Programming Optimization Problem

Constraints	Definition for Optimization Problem

Equality Constraints for Predictive Control

In the quadratic programming problem are the equality restrictions defined; however, they are not so commonly used in predictive-control applications. Definitions of inequality constraints in Table 1 are converted to expressions, as can be seen in Table 2.

Table 2. Definition of Equality Constraints for Quadratic Programming Optimization

Equality Value	Definition for Optimization Problem

By these definitions in Table 2, some parts of the regulation can be set, e.g. in case of some sampling periods. However, the equality will not be suitable at the whole time-range. The direct settings of the values of the signals can be restricted in this way only using constraints. This approach can be suitable in process control.

Results

Thermal laboratory model (Fig. 3) was identified by the least squares method to the form (11) and converted to the state-space model (12). The input signal is power [%] and the output variable is temperature [°C].

(11)

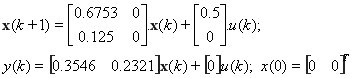  (12)

Fig. 3 Controlled Thermal Laboratory System (12)

The step response of the system (11) was given by the state-space equation (3) and compared in Fig. 4 with the measured results.

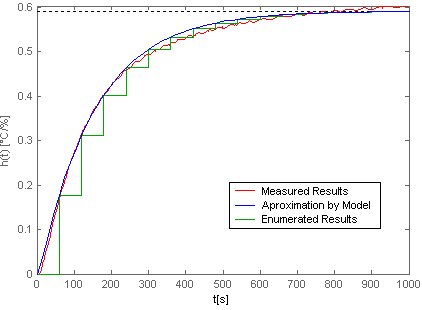
Fig. 4 Step Response of Controlled System

Algorithms of the predictive control were implemented in MathWorks: Matlab and Simulink environment with a connecting to the laboratory model. Its scheme (Fig. 5) was designed using the principles of the receding horizon strategy and the quadratic programming optimization approach.

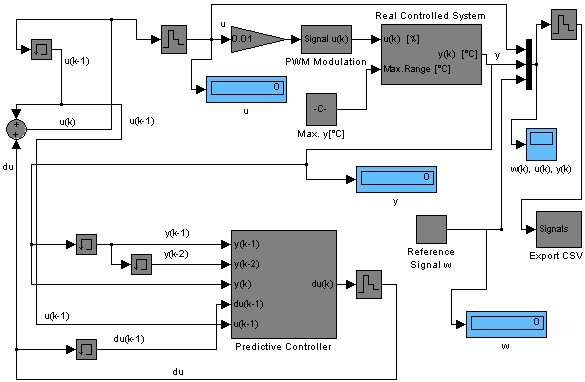
Fig. 5 Implementation of Predictive Control of Laboratory Model

The predictive control was used with the following settings of the horizon parameters: N1=1, Nu = 25, N2=28. The equality constraint du was activated from the first to the third sampling period with the value du=20 [%], as can be seen in Fig. 6.

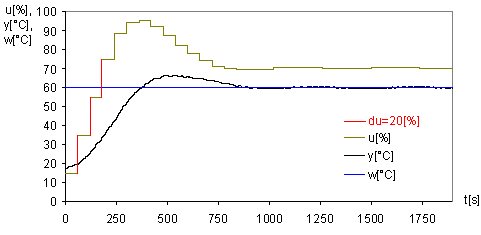
Fig. 6 Predictive Control with Equality Constraint du

Conclusion

The equality constraint was tested in the predictive control of the laboratory model. The definition was explained. This case of the variable restriction is not so widely discussed in the literature; however, these studies have been discussed yet. It is possible to use this approach in both optimization and predictive control. From the logical point of view it is possible to use the equality constraints in parts of a process control instead the whole time-range application. The requirements on the signal-values can be defined by this principle. The simulation was successfully compared with the practical results of testing in predictive-control.

Acknowledgement

The article was realized with financial support of IGA, Tomas Bata University in Zlín, Faculty of Applied Informatics number IGA/FAI/2014/002.

References

[1] Camacho, E. F., and C. Bordons. Model predictive control. London,Springer, 2007. ISBN 978-1-85233-694-3.
[2] Kwon, Wook Hyun. Receding horizon control: model predictive control for state models, London, Springer, 2005. ISBN 1-84628-024-9.
[3] Wang, Liuping. Model Predictive Control System Design and Implementation Using MATLAB. London: Springer-Verlag Limited, 2009. ISBN 978-1-84882-330-3.
[4] Huang, Sunan. Applied predictive control, London, Springer, 2002. ISBN 1852333383.
[5] Dostál, Zděnek. Optimal Quadratic Programming Algorithms: With Applications to Variational Inequalities (Springer Optimization and Its Applications). Springer, 2009. ISBN 978-0387848051.
[6] Lee, G. M., Tam, N. N., and N. D. Yen. Quadratic Programming and Affine Variational Inequalities: A Qualitative Study, Springer, 2005. ISBN 0-387-24277-5.
[7] D. G. Luenberger, and Y. Ye. Linear and nonlinear programming. New York: Springer, 2008. ISBN 978-0-387-74502-2.
[8] Clarke, D.W., and Scattolini, R. „Constrained receding-horizon predictive control," Control Theory and Applications, IEE Proceedings D , vol.138, no.4, pp.347,354, Jul 1991.
[9] Chisci, L., Lombardi, A., Mosca, E., and J.A. Rossiter, State-space approach to stabilizing stochastic predictive control, International Journal of Control, 65 (4), pp. 619-637. 1996.