An Overview on the Chaotic Lozi Map Enhanced PSO Algorithm with Inertia Weight

Michal Pluhacek, Roman Senkerik, Ivan Zelinka

Tomas Bata University in Zlin
Faculty of Applied Informatics
Nam T.G. Masaryka 5555, 760 01 Zlin
Czech Republic

pluhacek@fai.utb.cz, senkerik@fai.utb.cz, zelinka@fai.utb.cz

 

Abstract: The paper presents an overview on the utilization of chaotic Lozi map based chaos number generator to enhance the performance of PSO algorithm. Some previously published results are presented, reevaluated and discussed. One year of research is covered in this overview.

Keywords: Evolutionary algorithms, Particle swarm, Optimization, Swarm intelligence, Chaos

1 Introduction

PSO algorithm is one of evolutionary algorithms (class of soft computing methods that are inspired by nature). In recent years, various evolutionary algorithms were designed and used with great results in many areas of optimization [1-5]. More recently some studies indicated that using of chaotic number generators may improve the performance of evolutionary optimization algorithms on such tasks as PID controller design [6-8] or fuzzy modelling of an experimental thermal-vacuum system [9].

This overview covers one year of research and summarizes the progress and obtained results. Firstly, Particle swarm optimization algorithm is explained. The next sections are aimed on the description of used chaotic systems and benchmark test functions. Results analysis and conclusion follow afterwards.

2 Particle Swarm Optimization Algorithm

Particle swarm optimization (PSO) algorithm is based on the natural behavior of birds and fishes. It was firstly introduced by Eberhart and Kennedy in 1995 [1-3] as an alternative to genetic algorithms [4] and differential evolution [5].

In each generation, a new location of a particle is calculated based on its previous location and velocity (or “velocity vector”). One of PSO algorithm disadvantages is the rapid acceleration of particles which causes them abandoning the defined area of interest. For this reason, several modifications of PSO were introduced to handle with this problem. Main principles of PSO algorithm and its modifications are well described in [1,2] and [10].

Within this research, chaos driven PSO strategy with inertia weight was used. The selection of inertia weight modification of PSO was based on numerous previous experiments. Default values of all PSO parameters were chosen according to the recommendations given in [1,2] and [10].

Inertia weight is designed to influence the velocity of each particle differently over the time [10]. In the beginning of the optimization process, the influence of inertia weight factor w is minimal. As the optimization continues, the value of w is decreasing, thus the velocity of each particle is decreasing, since w is always the number < 1 and it multiplies previous velocity of particle in the process of new velocity value calculation. Inertia weight modification of PSO strategy has two control parameters wstart and wends. New w for each generation is then given by Eq. 1, where i stand for current generation number and n for total number of generations.

(1)

Chaos driven number generator is used in the main PSO formula (Eq. 2) that determines new “velocity”, thus the position of each particle in next generation (or migration cycle).

(2)

Where:

v(t+1) – New velocity of particle.

v(t) – Current velocity of particle.

c1,c2 – Priority factors.

pBest – Best solution found by particle.

gBest – Best solution found in population.

x(t) – Current position of particle.

Rand – Random number, interval <0,1>. Within Chaos PSO algorithm, the basic inbuilt computer (simulation software) random generator is replaced with chaotic generator (in this case, by using of Lozi map).

New position of the particle is then given by Eq. 3, where x(t+1) represents the new position:

(3)

3 Lozi Map

The Lozi map is a simple discrete two-dimensional chaotic map. The Lozi map is depicted in Fig. 1. The map equations are given in Eq. 4 and 5. The parameters used in this work are: a = 1.7 and b = 0.5 as suggested in [11].

(4)

(5)

Fig. 1: Lozi map

4 Performance Overview

In previous study [12] typical test functions were used to determine the impact of chaotic Lozi map on the performance of PSO algorithm and observe the impact on the behaviour of the particles in the population. These test functions are described in following section 4.1. They were chosen as good examples of both unimodal and multi-modal problems.

4.1Test functions

The First De Jong`s function is given by Eq. 6 and depicted in Fig. 2.

(6)

Function minimum:

Position for En: (x1,x2…xn) = En: (x1,x2…xn) = (0,0,…, 0)

Value for En: y = 0

The Second De Jong`s function is given by Eq. 7 and depicted in Fig. 3.

(7)

Function minimum:

Position for En: (x1,x2…xn) = (1,1,…,1)

Value for En: y = 0

Rastrigin`s function is given by Eq. 8 and depicted in Fig. 4.

(8)

Function minimum:

Position for En: (x1,x2…xn) = (0,0,…,0)

Value for En: y = 0

Schwefel`s function is given by Eq. 9 and depicted in Fig. 5.

(9)

Function minimum:

Position for En: (x1,x2…xn) = (420.969, 420.969,…, 420.969)

Value for En: y = -418.983 * dimension

Fig. 2: De Jongs`s first function in 3D	Fig. 3: De Jongs`s second function in 3D
Fig. 4: Rastrigin`s function in 3D	Fig. 5: Schwefel`s function in 3D

4.2. Results and Analysis

During the time period that is covered in this overview several experiments were undertaken and analyzed. At first 30 runs of both canonical PSO and Lozi map enhanced PSO were made on all four functions described above. From these 30 runs statistical indicators were derived. Most important of these indicators was the median. As can be seen on Fig. 6, for five different dimension settings (for full experiment setup see [12]), the Lozi map enhanced PSO algorithm was usually able to obtain better median values than the canonical PSO with inertia weight. The next step was an analysis of the history of gBest (very similar to best individual tracking in other EAs). From Fig. 7 and 8 (history of 30 runs on Schwefel´s function) it is clear, that Lozi map implementation in PSO seems to lead to faster convergence to the global optimum.

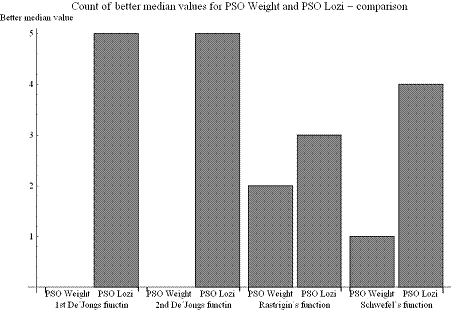
Fig. 6: PSO Weight and PSO Lozi results comparison

Fig. 7: History of best CF value during 2000 generations (30 separate runs) – PSO Weight

Fig. 8: History of best CF value during 2000 generations (30 separate runs) – PSO Lozi

During the research the results of PSO with Lozi map implementation were compared to those of DE and also to results of PSO with other chaotic maps (Dissipative standard map and Arnold´s cat map). At first, it seemed that the DE is easily archiving better results than all PSO modifications. It was however only question of proper algorithm settings. PSO performance on given number of iterations depends on the size of population much more than the performance of DE. This can be seen on Fig. 9 where the dependence of algorithm performance on the population size is displayed. It is easy to see, that if the number of iterations is fixed than with increasing population size the performance of PSO is improving significantly and furthermore that the performance of DE is actually worse, that is given by different inner principles of both algorithms.

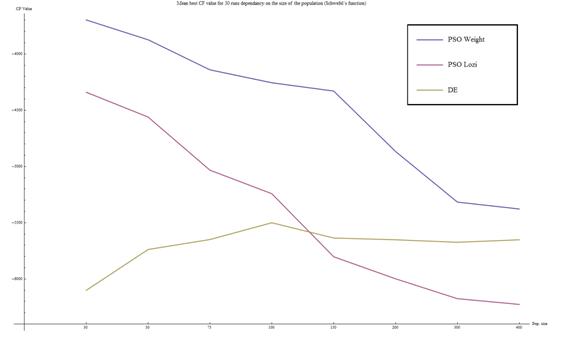
Fig. 9: PSO Weight, PSO Lozi and DE – influence of population size – Schwefel´s function

Finally, as mentioned above, some other chaotic maps were implemented into PSO and results of these algorithms were compared with those of Lozi map enhanced PSO. Typical results summary is depicted on Fig. 10 in this case for Schwefel´s function. The performance of PSO with Lozi map was usually the best.

Fig. 10: History of mean best CF value for 30 runs – comparison – Schwefel´s function

5 Conclusion

In this overview the research on Lozi map enhanced PSO with inertia weight was presented. The aim was to inform and highlight some crucial findings. Lozi map seems to have significant impact on the performance of PSO algorithm and the better understanding of this phenomenon is the object of future research.

Acknowledgement: This work was supported by European Regional Development Fund under the project CEBIA-Tech No. CZ.1.05/2.1.00/03.0089, and by Internal Grant Agency of Tomas Bata University under the project No. IGA/FAI/2012/037.

References:

[1] Kennedy, J.; Eberhart, R., "Particle Swarm Optimization". Proceedings of IEEE International Conference on Neural Networks. IV., 1995, pp. 1942–1948

[2] Eberhart, R., Kennedy, J., Swarm Intelligence, The Morgan Kaufmann Series in Artificial Intelligence, Morgan Kaufmann, 2001.

[3] Dorigo, M., Ant Colony Optimization and Swarm Intelligence, Springer, 2006.

[4] Goldberg, David E., Genetic Algorithms in Search Optimization and Machine Learning. Addison Wesley, 1989, p. 41, ISBN 0201157675.

[5] Storn, R., Price, R., Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces, Journal of Global Optimization 11, 1997, pp. 341–359.

[6] Davendra, D., Zelinka, I., Senkerik, R., “Chaos driven evolutionary algorithms for the task of PID control”, Computers & Mathematics with Applications, Volume 60, Issue 4, 2010, pp 1088-1104, ISSN 0898-1221.

[7] Pluhacek M., Senkerik R., Davendra D., Zelinka I., Designing PID Controller For DC Motor System By Means Of Enhanced PSO Algorithm With Discrete Chaotic Lozi Map, In: Proceedings of the 26th European Conference on Modelling and Simulation, ECMS 2012, pp. 405 - 409, 2012, ISBN 978-0-9564944-4-3.

[8] Pluhacek M., Senkerik R., Davendra D., Zelinka I., PID CONTROLLER DESIGN FOR 4TH ORDER SYSTEM BY MEANS OF ENHANCED PSOALGORITHM WITH LOZI CHAOTIC MAP, In: Proceedings of the 18th International Conference on Soft Computing, MENDEL 2012, pp. 35 - 39, 2012, ISBN 978-80-214-4540-6.

[9] Araujo, E., Coelho, L., Particle swarm approaches using Lozi map chaotic sequences to fuzzy modelling of an experimental thermal-vacuum system, Applied Soft Computing, v.8 n.4, p.1354-1364, September, 2008

[10] Nickabadi, A., Ebadzadeh, M. M., Safabakhsh, R., A novel particle swarm optimization algorithm with adaptive inertia weight, Applied Soft Computing, Volume 11, Issue 4, June 2011, Pages 3658-3670, ISSN 1568-4946

[11] Sprott, J. C., “Chaos and Time-Series Analysis“, Oxford University Press, 2003

[12] Pluhacek M., Budikova V., Senkerik R., Oplatkova Z., Zelinka I., EXTENDED INITIAL STUDY ON THE PERFORMANCE OF ENHANCED PSO ALGORITHM WITH LOZI CHAOTIC MAP, Advances in Intelligent Systems and Computing, 1, Volume 192, Nostradamus: Modern Methods of Prediction, Modeling and Analysis of Nonlinear Systems, pp. 167 - 177, 2012, ISBN 978-3-642-33226-5.