Petr Dostál, Jiří Vojtěšek, and Vladimír Bobál
Department of Process Control, Faculty of Applied Informatics
Tomas Bata University in Zlin
Nad Stráněmi 2911, Zlín 760 05, Czech republic
E-mail: dostalp@fai.utb.cz
Abstract
The paper deals with simulation of continuous-time adaptive control of a continuous stirred tank reactor (CSTR). The control design is based on approximation of a nonlinear model of the process by a continuous-time external linear model.with parameters estimated using a corresponding delta model. The control system with two feedback controllers is considered. The controller design is based on the polynomial approach and the pole assignment method. The adaptive control is tested by simulations on the nonlinear model of the CSTR with a consecutive exothermic reaction.
Introduction
Continuous stirred tank reactors (CSTRs) belong to a class of nonlinear systems where both steady-state and dynamic behaviour are nonlinear. Their models are derived and described in e.g. (Ogunnaike and Ray 1994; Schmidt 2005; Corriou 2004). The process nonlinearities may cause difficulties when controlling using conventional controllers with fixed parameters. One possible method to cope with this problem is using adaptive strategies based on an appropriate choice of an external linear model (ELM) with recursively estimated parameters. These parameters are consequently used for parallel updating of controller‘s parameters.
The control itself can be either continuous-time or discrete. Experiences of authors in the field of control of nonlinear technological processes indicate that the continuous- time (CT) approach gives better results when controlling processes with strong nonlinearities.
For the CT ELM parameters estimation, either the direct method or application of an external delta model with the same structure as the CT model can be used (Dostál et al. 2004). In this paper, an approach based on the delta model was applied.
The basics of delta models have been described in e.g. (Middleton and Goodwin 1990; Mukhopadhyay et al. 1992; Goodwin et al. 2001). Although delta models belong into discrete models, they do not have such disadvantages connected with shortening of a sampling period as discrete z-models. In addition, parameters of delta models can directly be estimated from sampled signals. Moreover, it can be easily proved that these parameters converge to parameters of CT models for a sufficiently small sampling period (compared to the dynamics of the controlled process). Complete description and experimental verification can be found in (Stericker and Sinha 1993).
This contribution presents in brief a procedure of a CSTR control design and, consequently, the control simulation results. The parameters of the CT ELM are obtained via corresponding delta model parameter estimation. The control system with two feedback controllers is used according to (Ortega and Kelly 1984; Dostál et al. 2007). This set-up gives better control results for the reference tracking than the use of only a feedback controller. Input signals for the control system are considered as step functions. The resulting continuous-time controllers derived using polynomial and pole assignment methods (Kučera 1993) guarantee stability of the control system, asymptotic tracking of step references and step load disturbances attenuation. The simulations are performed on a nonlinear model of the CSTR with a consecutive exothermic reaction.
Model of the plant
Consider a CSTR with the first order consecutive exothermic reaction according
to the scheme
and with a perfectly mixed cooling jacket. Using the usual simplifications, the
model of the CSTR is described by four nonlinear differential equations
(1)
(2)
(3)
(4)
with initial conditions
,
,
and
.
Here, t is the time, c are concentrations, T are temperatures,
V are volumes, r are densities, cp are specific heat capacities,
Q are volumetric flow rates, Ah is the heat exchange surface
area and U is the heat transfer coefficient. The subscripts are denoted (.)r
for the reactant mixture, (.)c for the coolant, (.)f
for feed (inlet) values and the superscript (.)s for
steady-state values. The reaction rates and the reaction heat are expressed as
(5)
(7)
where k0 are pre-exponential factors, E are activation energies and (-DHr) are in the negative considered reaction entalpies. The values of all parameters, feed values and steady-state values in the operating point (initial conditions for (1) — (4)) are given in Table 1.
Table 1. Parameters, inlet values and initial conditions (operating point).
|
Vr = 1.2 m3 Vc = 0.64 m3 A = 5.5 m2 |
Qrs = 0.08 m3min-1 Qcs = 0.073 m3min-1 |
rr = 985 kg m-3 rc = 998 kg m-3 |
cpr = 4.05 kJ kg-1K-1 cpc = 4.18 kJ kg-1K-1 U = 43.5 kJ m-2min-1K-1 |
|
k10 = 5.616 . 1016 min-1 k20 = 1.128 . 1018 min-1 |
E1/ R = 13477 K E2/ R = 15290 K |
|
|
|
cAf = 2.85 kmol m-3 Tf = 323 K |
cBf = 0 kmol m-3 Tcf = 293 K |
cAs = 1.374 kmol m-3 Trs = 327.1 K |
cbs = 1.361 kmol m-3 Tcs = 308.0 K |
In term of the practice, only the coolant flow rate can be taken into account as the control input. On behalf of selection of a suitable controlled output, the dynamic charakteristics were computed in the neighbourhood of the operating point. The input and both outputs were considered as deviations from steady values. The deviations are denoted as follows:
,
,
The responses in Figs. 1 and 2 show a better applicability of the reactant temperature
as the controlled output in comparison with the component B output concentration
having in this regard very unfavourable properties.
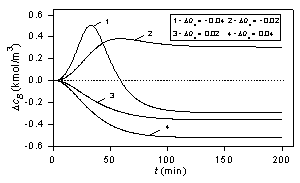
Figure 1: Component B output concentration step responses. Figure 2: Reactant temperature step responses.
CT and DELTA external linear model
For the control purposes, the controlled output and the control input were defined as
.
(7)
These expressions enable to obtain variables of approximately the same magnitude.
Taking into account curves in Fig. 2, the second order CT ELM can be chosen in the form of the second order linear differential equation
(8)
or, in the transfer function representation as
.
(9)
Establishing the d operator
(10)
where q is the forward shift operator and T0 is the sampling period, the delta ELM corresponding to (8) takes the form
(11)
where
is
the discrete time.
When the sampling period is shortened, the delta operator approaches the derivative
operator, and, the estimated parameters
reach the parameters a, b of the CT model as shown in (Stericker and
Sinha 1993).
DELTA model parameter estimation
Substituting
,
equation (11) may be rewriten to the form
(12)
Establishing the regression vector
(13)
where
,
,
the vector of delta model parameters
(14)
is recursively estimated from the equation
(15)
where
.
(16)
The recursive estimation of delta model parameters was performed with the sampling interval T0 = 0.5 min. Here, the recursive identification method with exponential and directional forgetting according to (Rao and Unbehauen 2005; Bobál et al. 2005) was used.
Constrol system description
The control system with two feedback controllers is depicted in Fig. 3. In the scheme, w is the reference signal, v denotes the load disturbance, e is the tracking error, u0 is the output of the controller, y is the controlled output and u is the control input.
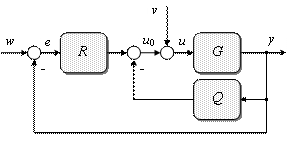
Figure 3: Control system with two feedback controllers.
In general therms, G represents the ELM with the transfer function
(17)
and Q and R are feedback controllers with transfer functions
,
(18)
where
are
polynomials in s.
Both w and v are considered to be step functions with transforms
,
.
(19)
Application of polynomial method
The controller design described in this section appears from the polynomial approach. General conditions required to govern the control system properties are formulated as strong stability (in addition to the control system stability, also the stability of controllers is required), internal properness, asymptotic tracking of the reference and load disturbance attenuation.
The procedure to obtain admissible controllers can be briefly described as follows:
Establish the polynomial t as
.
(20)
Then, the control system stability is ensured when polynomials
and t are given by a solution of the polynomial Diophantine equation
(21)
with a stable polynomial d on the right side. Evidently, the roots of d determine poles of the closed-loop.
Further, the asymptotic tracking and load disturbance attenuation are provided
by polynomials
and
having the form
,
.
(22)
Subsequently, the transfer functions of controllers take forms
,
.
(23)
A stable polynomial p(s) in denominators of (23) ensures the stability of controllers.
The control system satisfies the condition of internal properness when the transfer functions of all its components are proper. Consequently, the degrees of polynomials q and r must fulfill inequalities
,
.
(24)
Now, the polynomial t can be rewritten into the form
.
(25)
Taking into account solvability of (21) and conditions (24), the degrees of polynomials in (21) and (24) can be easily derived as
,
,
,
.
(26)
Denoting deg a = n, polynomials t, r and q have forms
,
,
(27)
where their coefficients fulfill equalities
,
for
(28)
Then, unknown coefficients ri and qi can
be obtained by a choice of selectable coefficients
such that
,
for
.
(29)
The coefficients bi split a weight between numerators of transfer functions Q and R. With respect to (23) and (29), it may be expected that higher values of bi will speed up control responses to step references.
Remark: If
for
all i, the control system in Fig. 1 simplifies to the 1DOF control configuration.
If
for all i and both reference and load disturbance are step functions, the
control system corresponds to the 2DOF control configuration.
The controller parameters then follow from solution of the polynomial equation (21) and depend upon coefficients of the polynomial d.
Now, for the second order model (9) with
,
the numerators in (23) take forms
,
(30)
where
,
,
,
.
(31)
Pole assingment
A required control quality can be achieved by a suitable determination of the polynomial d on the right side of (21).
In this paper, the polynomial d is chosen as a product of two stable factors
.
(32)
Here, g is the third order stable polynomial
(33)
given by spectral factorization
(34)
and asterisk denotes a conjugate polynomial.
Note that the spectral factorization (34) is well known from the LQ control theory. There g appears from a claim of minimization of the cost function
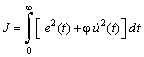(35)
where j is the weight coefficient.
The polynomial n is the second order stable polynomial
(36)
resulting from spectral factorization
(37)
The form (32) leads to strictly proper controllers with transfer functions
,
.
(38)
Note that the choice of d in the form (32) provides the control of a good quality for aperiodic controlled processes.
Now, it follows from the above introduced procedure that the parameters of both controllers depend upon coefficients ß as well as upon the parameter j which affects the closed-loop poles. Consequently, tuning of the controllers can be performed by a suitable choice of selectable parameters ß and j. The adaptive control system is shown in Fig. 4.
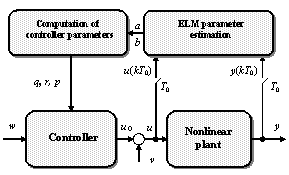
Figure 4: Adaptive control with delta ELM parameter estimation.
Simulation results
For the start (the adaptation phase), a P controller with a small gain was used in all simulations.
The effect of the parameter j on the control responses in the 1DOF structure is transparent from Figs. 5 and 6. Here, three values j were selected. The control results show sensitivity of the controlled output and control input to j. An decreasing j leads to overshoots of the controlled output and higher values and changes of the control input.
The control responses for b1 = ß2 = 1 (the 1DOF structure), b1 = ß2 = 0.5 and b1 = ß2 = 0 (the 2DOF structure) with the same j are compared in Figs. 7 and 8. The presented results show that by a suitable choice of parameters b, the control responses of a good quality can be achieved. Moreover, decreasing values b lead to smaller control input changes. This fact can be important for a practical control where greater input changes may be undesirable.
The simulated control responses for b2 = 0 and different values b1 are shown in Figs. 9 and 10. The effect of the parameter b1 is evident. Its increase speeds up the control, but, it can lead to overshoots of the controlled output and to higher control input changes (derivatives).
Figure 5: Controlled outputs for various j (1DOF). Figure 6: Control inputs for various j (1DOF).
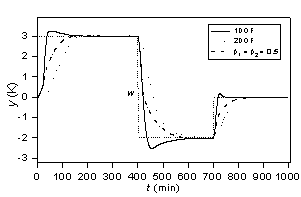
Figure 7: Controlled outputs for various b1, b2 (j = 1). Figure 8: Control inputs for various b1, b2 (j = 1).
at times
and
are
considered. The controller parameters were estimated only in the first (tracking)
interval t < 190 min. During interval t ł 190 min, fixed parameters
were used. The disturbances and controlled output responses are shown in Fig. 11.
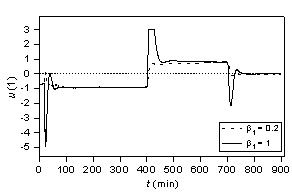
Figure 9: Controlled outputs for various b1 (j = 1). Figure 10: Control inputs for various b1 (j = 1).
Figure 11: Step disturbance attenuation (1DOF, j = 1).
Conclusions
An objective of the article was to verify by simulations an adapteve control algorithm derived for a continuous stirred tank reactor. The presented strategy uses two feedback controllers and enables to create an effective control algorithm. This algorithm is based on an alternative continuous-time external linear model with parameters obtained through recursive parameter estimation of a corresponding delta model. Both resulting continuous-time controllers are derived using the polynomial approach and given by a solution of a polynomial Diophantine equation. Tuning of their parameters is possible either via the parameter affecting the closed-loop poles or by a choice of selectable coefficients splitting a weight between numerators of controllers' transfer functions. The presented method has been tested by computer simulation on the nonlinear model of the CSTR with a consecutive exothermic reaction. The results demonstrate the applicability of the presented control strategy.
Acknowledgment
This work was supported by the Ministry of Education of the Czech Republic under the grant MSM 7088352101.
References
Aktuální číslo
Odborný vědecký časopis Trilobit | © 2009 - 2024 Fakulta aplikované informatiky UTB ve Zlíně | ISSN 1804-1795
= 4.8 . 104 kJ kmol-1
=
2.2 . 104 kJ kmol-1